 |
Ganzrationale Funktionen Globalverhalten - Level 1 - Grundlagen - Blatt 1 |
| Dokument mit 52 Aufgaben |
Aufgabe A1 (10 Teilaufgaben)
| Gib von der ganzrationalen Funktion f den Grad, die Koeffizienten und das Absolutglied an. |
 |
 Eine Frage stellen... |
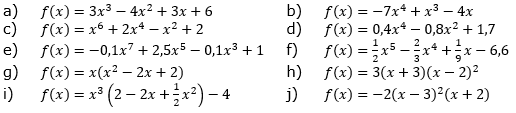Fehler melden...Aufgabe A2 (8 Teilaufgaben)
| Überlege, welche Vorzeichen die Funktionswerte f(500) und f(-500) haben könnten. |
 |
| Eine Frage stellen... |
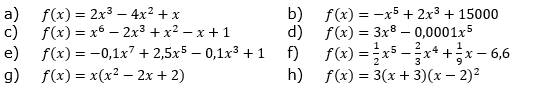Aufgabe A3 (8 Teilaufgaben)
| Gib eine Funktion h mit h(x)=an xn an, die das Verhalten der Graphen von f für die Werte von x→±∞ beschreibt. |
 |
| Eine Frage stellen... |
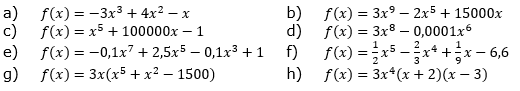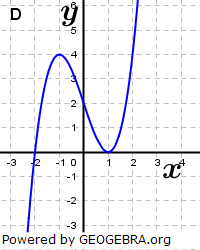
Aufgabe A4 (4 Teilaufgaben)
| Ordne den Funktionsgleichungen die Graphen zu und begründe. |
 |
    |
| Eine Frage stellen... |
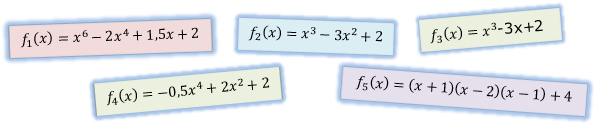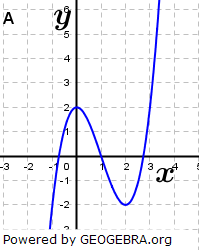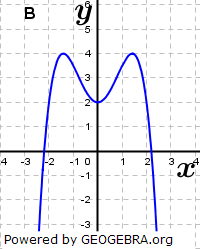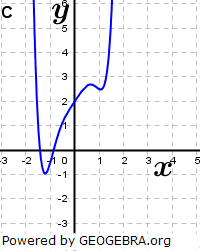Aufgabe A5 (8 Teilaufgaben)
| Gib eine Funktion an, die das Verhalten des Graphen von f nahe 0 beschreibt. |
 |
| Eine Frage stellen... |
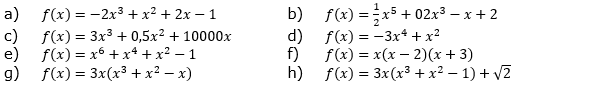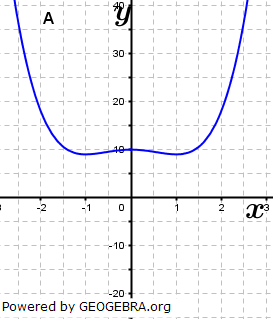
Aufgabe A6 (4 Teilaufgaben)
| Ordne den Funktionsgleichungen die Graphen zu und begründe. Es sind zwei Funktionen zu viel angegeben. Skizziere von diesen Funktionen die Graphen. |
 |
    |
| Eine Frage stellen... |
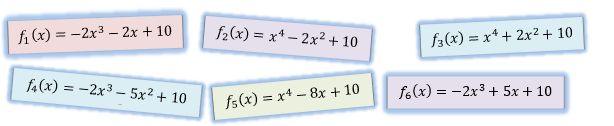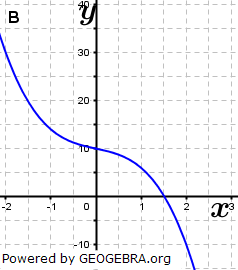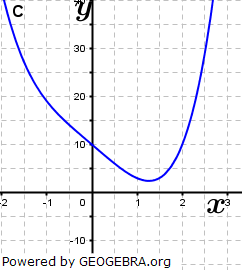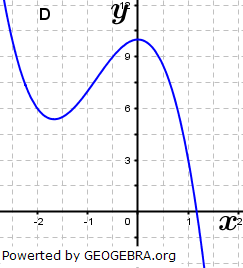Aufgabe A7 (8 Teilaufgaben)
| Mithilfe der fünf Zahlen -2; -1; 0; 1 und 2 als Koeffizienten können verschiedene, ganzrationale Funktionen gebildet werden, wobei in jeder Funktionsgleichung die genannten Koeffizienten nur einmal vorkommen dürfen, aber jeder einzelne vorkommen muss. Beispiele: |
|
| f(x)=1⋅x4+0⋅x3-1∙x2+2∙x-1 oder | |
| f(x)=0⋅x4+2⋅x3-2∙x2+1∙x-1 | |
| Bestimme eine derartige Funktion so, dass | |
| a) | der Graph von f die y-Achse im Punkt P(0|1) schneidet, |
| b) | der Graph von f durch den Ursprung geht, |
| c) | f(-1)=6 ist, |
| d) | der Graph von f aus dem dritten in den ersten Quadranten verläuft, |
| e) | der Graph von f aus dem vierten in den zweiten Quadranten verläuft, |
| f) | die Funktionswerte von f für x→|∞| gegen Unendlich streben, |
| g) | das Verhalten von f nahe 0 durch die Funktion g(x)=x-2 beschrieben wird, |
| h) | das Verhalten von f für sehr große und sehr kleine Werte von x durch die Funktion h(x)=2x4 beschrieben wird. |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Ganzrationale Funktionen Globalverhalten - Level 1 - Grundlagen - Blatt 1 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
