|
Besondere Lage ganzrationaler Funktionen - Level 3 - Expert - Blatt 5 |
| Dokument mit 8 Aufgaben |
Aufgabe A1
Gegeben ist die Funktion f mit 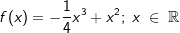 . .Bestimme die Ursprungsgerade, die das Schaubild K von f außerhalb des Ursprungs berührt. Gib den Berührpunkt an. |
| |
Aufgabe A2
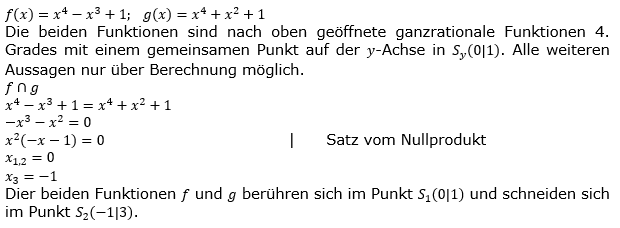
Gegeben sind die Funktionen f und g mit f(x)=x4-x3+1 und g(x)=x4+x2+1; 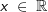 . .Mache Aussagen über die gegenseitige Lage der zugehörigen Kurven. Bestätige deine Aussage durch Rechnung. |
| |
Aufgabe A3
K ist das Schaubild von f mit f(x)=x2(x-3);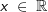 . .Untersuche die gegenseitige Lage von K und G von g mit g(x)=ax2 in Abhängigkeit von a. |
| |
Aufgabe A4 (4 Teilaufgaben)
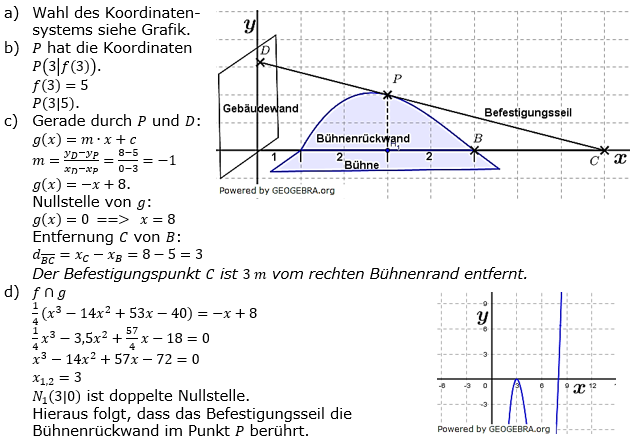
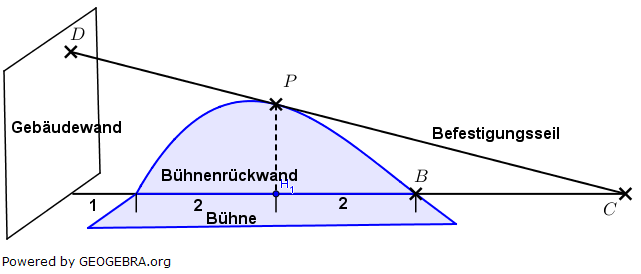 Für ein Openair-Konzert soll rechts neben einer Gebäudewand eine Bühne errichtet werden. Die Bühnenrückwand soll die Form eines Bogens haben (siehe Abbildung). Für ein Openair-Konzert soll rechts neben einer Gebäudewand eine Bühne errichtet werden. Die Bühnenrückwand soll die Form eines Bogens haben (siehe Abbildung).In einem geeigneten Koordinatensystem wird der Bogen durch den im I. Quadranten verlaufenden Teil der Funktion f mit 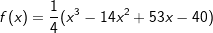 , (1 ???????? ≜ 1 ????) beschrieben. , (1 ???????? ≜ 1 ????) beschrieben. |
|
| Zur Sicherung der Bühnenkonstruktion wird ein Seil vom Punkt D in 8 m Höhe an der Gebäudewand zum Punkt C auf dem Erdboden gespannt. Das Seil berührt die Bühnenrückwand im Punkt P. | |
| a) | Wie muss das Koordinatensystem hinzugefügt werden? Begründe deine Ihre Wahl. |
| b) | Bestimme die Koordinaten von P. |
| c) | Berechne, in welcher Entfernung zum rechten Bühnenrand B sich der Befestigungspunkt C befindet. |
| d) | Bei der rechnerischen Bestimmung von P ergab sich eine doppelte Schnittstelle in x=3. Formuliere einen möglchen Ansatz und interpretiere die Lösung. |
| |
Aufgabe A5
| Die Grafik rechts zeigt einen Ausschnitt aus dem Graphen K von f mit | 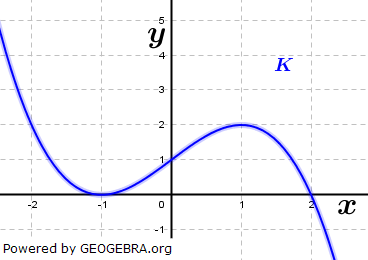 |
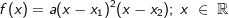 . . |
|
| Ermittle a, x1 und x2 aus der Abbildung. Welche Paralellen zur x-Achse haben mit f einen, zwei oder drei gemeinsame Punkte? |
| |
| Du befindest dich hier: |
| Besondere Lage ganzrationaler Funktionen - Level 3 - Expert - Blatt 5 |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021