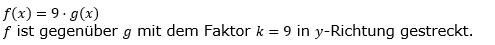 |
Quadratische Funktionen (Parabeln) Level 2 - Fortgeschritten - Aufgabenblatt 4 |
| Dokument mit 34 Aufgaben |
Aufgabe A1
| Eine quadratische Funktion f hat ihren Scheitel in S(0|6) und schneidet die x-Achse im Punkt P(2√3|0). Bestimme die Funktionsgleichung und zeichne den Graphen. |
 Eine Frage stellen... |
Fehler melden...Aufgabe A2 (6 Teilaufgaben)
| Gegeben sind die Funktionsgleichungen folgender Parabeln: | ||||||
| 1. | Bestimme die Scheitelform und den Scheitelpunkt. | |||||
| 2. | Berechne die Achsenschnittpunkte. | |||||
| 3. | Beschreibe schrittweise, wie f aus der Normalparabel entsteht und wie sie geöffnet ist. | |||||
| 4. | Zeichne den Graphen von f in ein geeignetes Koordinatensystem. | |||||
| a) | f(x)=x2-4x+2 | b) | f(x)=x2+4x+2 | c) | f(x)=x2-4x+3 | |
| d) | f(x)=x2+8x-9 | e) |  |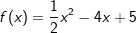
f) |  |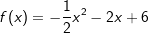
|
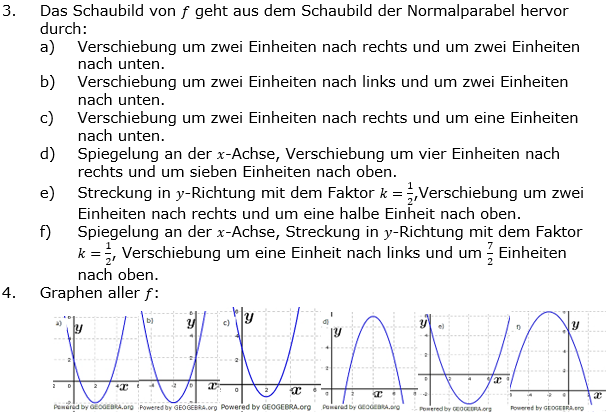
| Eine Frage stellen... |
Aufgabe A3 (5 Teilaufgaben)
Gegeben ist die Funktionsgleichung einer Parabel mit  . |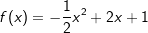
|
| a) | Berechne den Scheitelpunkt mithilfe der Scheitelform. |
| b) | Berechne die Achsenschnittpunkte. |
| c) | Die Parabel soll so verschoben werden, dass der Punkt der Parabel, der auf der y-Achse liegt durch den Punkt P(-3|-1) verläuft. Wie lautet die Funktionsgleichung p(x) der verschobenen Parabel? |
| d) | Wo schneiden sich beide Parabeln? |
| e) | Zeichne beide Parabeln in ein geeignetes Koordinatensystem. |
| Eine Frage stellen... |
Aufgabe A4 (2 Teilaufgaben)
| Der Kraftstoffverbrauch eines PKW hängt bekanntlich von der Geschwindigkeit ab. Durch Messungen wurde der funktionale Zusammenhang ermittelt. Es gilt: K(v)=0,002v2-0,18v+8,55 für v > 40. Dabei bedeutet K(v) der Kraftstoffverbrauch in Liter/100 km und v die Geschwindigkeit in km/h. |
|
| a) | Bei welcher Geschwindigkeit beträgt der Verbrauch genau 7 Liter auf 100 km? |
| b) | Bei welcher Geschwindigkeit ist der Kraftstoffverbrauch am geringsten? |
| Eine Frage stellen... |
Aufgabe A5 (3 Teilaufgaben)
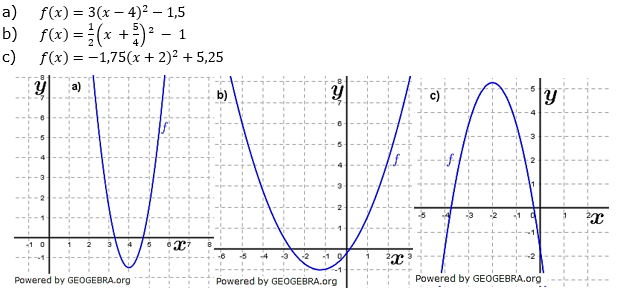
| Bestimme die Scheitelform der Parabeln und zeichne sie. | |
| a) | Die Normalparabel wird um 3 gestreckt, um 4 nach rechts und um 1,5 nach unten verschoben. Die Parabel ist nach oben geöffnet. |
| b) | Die Normalparabel wird um  gestaucht, um  nach links und um 1 nach unten verschoben. Die Parabel ist nach oben geöffnet. |
| c) | Die Normalparabel wird um 1,75 gestreckt, um 2 nach links und um 5,25 nach oben verschoben. Die Parabel ist nach unten geöffnet. |
| Eine Frage stellen... |
Aufgabe A6 (5 Teilaufgaben)
| Gegeben sind die quadratischen Funktionen f mit f(x)=-x2-3x; x ∈ R und g mit g(x)=0,5x(x+3); x ∈ R. | ||
| a) | Abgebildet sind die Graphen von f und g. Begründe ohne Rechnung, warum sich f und g auf der x-Achse schneiden. S(-1,5|2,25) ist der Scheitel von f. Gib den Scheitel von g an. |
|
| b) | Die Gerade x=u schneidet den Graphen von f im Punkt P und den Graphen von g im Punkt Q. Gib die Koordinaten von P und Q an. |  |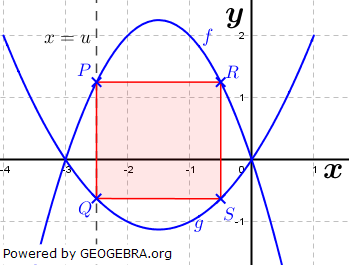
| c) | Für u ∈ ]-3;0[ ist die Strecke 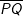 eine Seite eines Rechtecks, das den beiden Parabeln einbeschrieben ist. Bestimme den Inhalt des Rechtecks für u=-1 und den Umfang U in Abhängigkeit von u. |
|
| d) | Verschiebe die Parabel g in y-Richtung so, dass die verschobene Parabel den Graphen von f berührt. Bestimme die Koordinaten des Berührpunktes B. | |
| e) | Bestimme a so, dass f(a)-f(a+1)=4 ist. | |
| Eine Frage stellen... |
Aufgabe A7
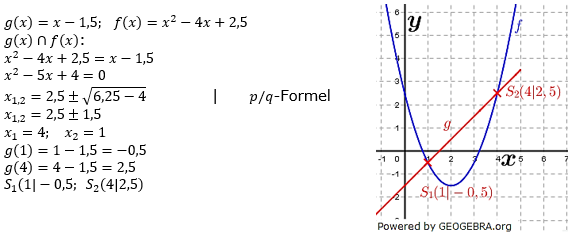
| Bestimme die Schnittpunkte der Geraden g(x)=x-1,5 mit der Parabel f(x)=x2-4x+2,5 rechnerisch. Kontrolliere dein Ergebnis graphisch. |
| Eine Frage stellen... |
Aufgabe A8
| Gib jeweils die Gleichung einer Parabel an, die mit der Parabel f(x)=x2+2x keinen, einen bzw. zwei verschiedene Schnittpunkte hat. |
| Eine Frage stellen... |
?
Aufgabe A10 (6 Teilaufgaben)
| Bei welcher der Folgenden Funktionen handelt es sich um quadratische Funktionen? | |||||
| a) | f(x)=x+1 | b) |  |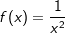
c) | f(x)=2x2+4+x3 |
| d) | f(x)=-4x2+5x+9 | e) |  |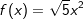
f) | f(x)=x2 |
| Eine Frage stellen... |
Aufgabe A11 (4 Teilaufgaben)
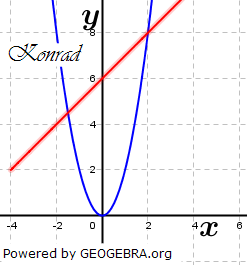
| Martina, Jutta und Konrad sollten als Hausaufgabe die Gleichung x2-2x-2=0 graphisch lösen. Sie sind dabei unterschiedlich vorgegangen, aber alle auf die gleichen Näherungslösungen x1≈-0,7 und x2≈2,7 gekommen. | |
   |
|
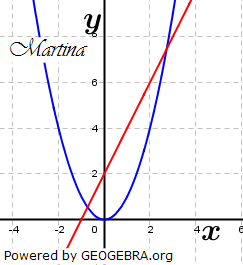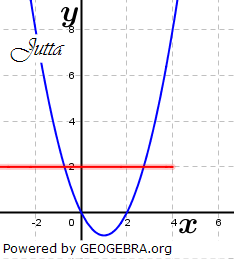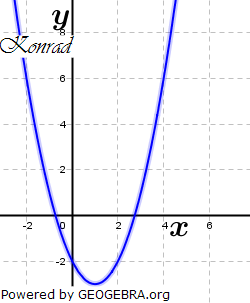| a) | Überprüfe die Näherungslösungen rechnerisch. |
| b) | Erläutere die Vorgehensweisen von Martina, Jutta und Konrad. |
| c) | Ermittle mit jedem Verfahren die Lösungen der Gleichung x2+3x+2=0. |
| d) | Jutta und Konrad sind von Martinas Methode begeistert und versuchen, damit die Gleichung 2x2-x-6=0 zu lösen. Sie gehen dabei aber unterschiedlich vor (siehe nachstehende Abbildungen). Welche Ergebnisse erhalten sie? Überprüfe rechnerisch. Wer von beiden ist deiner Meinung nach geschickter vorgegangen? Begründe. |
  |
|
| Eine Frage stellen... |
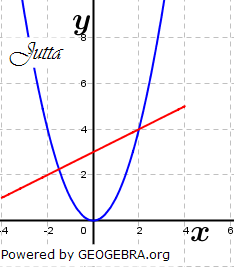| Du befindest dich hier: |
| Quadratische Funktionen (Parabeln) Level 2 - Fortgeschritten - Aufgabenblatt 4 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
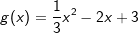