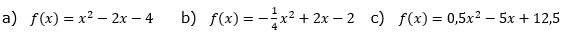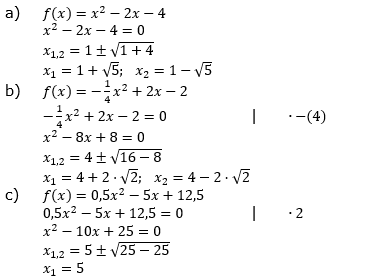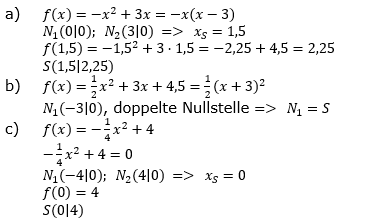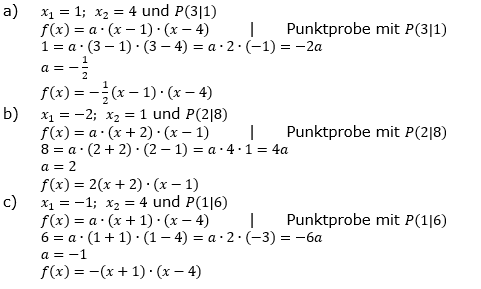 |
Quadratische Funktionen (Parabeln) Level 1 - Grundlagen - Aufgabenblatt 3 |
| Dokument mit 38 Aufgaben |
Aufgabe A1 (3 Teilaufgaben)
Eine Parabel hat ihren Scheitel in S und geht durch P. Bestimme den zugehörigen Funktionsterm in der Scheitelform und in der Hauptform. |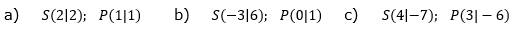
 Eine Frage stellen... |
| Stelle die Scheitelform auf mit f(x)=a(x-xS )2+yS und mache damit eine Punktprobe mit P zur Bestimmung von a. |
 Fehler melden... |
Aufgabe A2 (6 Teilaufgaben)
| Gegeben sind Hauptformen quadratischer Gleichungen. Darunter sind Karten mit der Nullstellenform von Funktionsgleichungen abgebildet. Finde zu den Gleichungen a) bis f) die passende Lösungskarte und bilde aus den Buchstaben ein Lösungswort.  |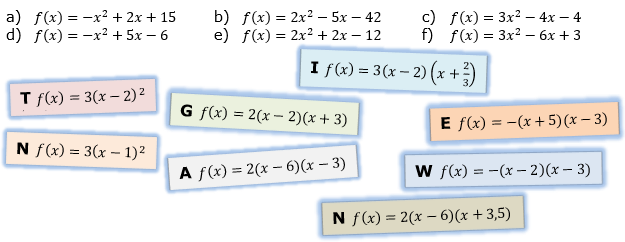
| Eine Frage stellen... |
| Ein Punkt liegt dann auf der Normalparabel (mit der Funktionsgleichung f(x)=x2), wenn mit einer Punktprobe eine wahre Aussage eintritt. Bei einer Punktprobe musst du den Ausdruck f(x) durch den y-Wert des Punktes ersetzen und den x-Wert in die Funktionsgleichung einsetzen. |
| Fehler melden... |
Aufgabe A3 (9 Teilaufgaben)
Schreibe den Funktionsterm in der Produktform und lies die Nullstellen ab, ohne zu rechnen. |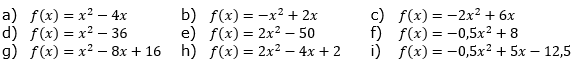
| Eine Frage stellen... |
| Stelle die Produktformel durch Ausklammern auf und ermittle daraus die Nullstellen. |
| Fehler melden... |
Aufgabe A4 (6 Teilaufgaben)
Gegeben ist die quadratische Funktion f. In welchen Bereichen sind die Funktionswerte positiv? |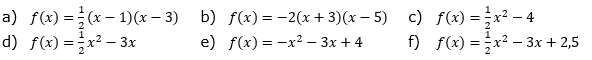
| Eine Frage stellen... |
| Bestimme die Nullstellen von und ermittle daraus den/die Bereich(e), in denen f(x) > 0 ist. Ist die Parabel nach oben geöffnet, sind die y-Werte im Intervall von -∞ bis zur linken Nullstelle, bzw. von der rechten Nullstelle bis +∞ positiv. Ist die Parabel nach unten geöffnet, sind die y-Werte im Intervall von der linken Nullstelle bis zur rechten Nullstelle positiv. |
| Fehler melden... |
| Nullstellen berechnest du mithilfe der sogenannten Mitternachtsformel. Du kannst hierfür sowohl die p/q-Formel als auch die abc-Formel verwenden. In diesem Portal wird ausschließlich die p/q-Formel verwendet. Bei Verwendung der p/q-Formel musst du darauf achten, dass der Koeffizient von x2 unbedingt 1 ist. Hierfür kannst du jederzeit durch Division der Gleichung mit dem eventuell vorhandenen Koeffizienten von x2 sorgen. |
| Fehler melden... |
Aufgabe A6 (3 Teilaufgaben)
Schreibe den Funktionsterm in Produktform, gib die Nullstellen ohne Rechnung an und bestimme den Scheitelpunkt. |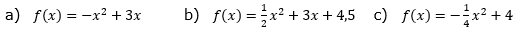
| Eine Frage stellen... |
Aufgabe A7
| Skizziere den Graphen der quadratischen Funktion f mit f(x)=-2x2+16x-24. Bestimme den Bereich, in denen der Graph positive Funktionswerte hat. |
| Eine Frage stellen... |
Aufgabe A8 (3 Teilaufgaben)
Der Graph einer quadratischen Funktion f schneidet die x-Achse in x1 und x2 und geht durch P. Bestimme den Funktionsterm. |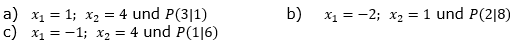
| Eine Frage stellen... |
| Stelle die Nullstellenformel f(x)=a∙(x-x1)∙(x-x2) mit x1 und x2 als Abszissenwerte der Nullstellen auf und mache dann eine Punktprobe mit P zur Berechnung von a. |
| Fehler melden... |
Aufgabe A9 (3 Teilaufgaben)
Für welche Werte von t hat die Funktion f genau eine Nullstelle? Wie muss t gewählt werden, damit es zwei (keine) Nullstellen gibt? |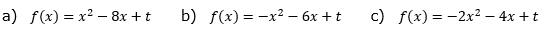
| Eine Frage stellen... |
| Berechne die Nullstellen der Funktion mit der p/q-Formel (alternativ abc-Formel) in Abhängigkeit von t. Prüfe dann die Diskriminante. Führen Werte von t zu einer positiven Diskriminante, so hat der Graph der Funktion zwei Nullstellen. Führen Werte von t zu einer Diskriminante gleich Null, so hat der Graph der Funktion eine Nullstelle. Führen Werte von t zu einer negativen Diskriminante, so hat der Graph der Funktion keine Nullstelle. |
| Fehler melden... |
Aufgabe A10
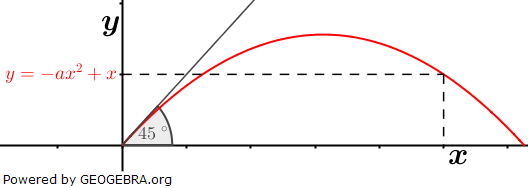 In einem Fußballspiel wird der Fußball mit 25 m/s unter einem Winkel von 45 ° schräg nach oben geschossen. Die parabelförmige Flugbahn kann mit der quadratischen Funktion f mitf(x)=-0,016x2+x beschrieben werden. Wo erreicht der Ball den höchsten Punkt, wo kommt er wieder auf dem Boden auf? |
| Eine Frage stellen... |
| Der höchste Punkt des Balls liegt im Scheitel des Graphen der Funktion. Der Ball trifft in der rechten Nullstelle wieder auf dem Boden auf. |
| Fehler melden... |
| Du befindest dich hier: |
| Quadratische Funktionen (Parabeln) Level 1 - Grundlagen - Aufgabenblatt 3 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
