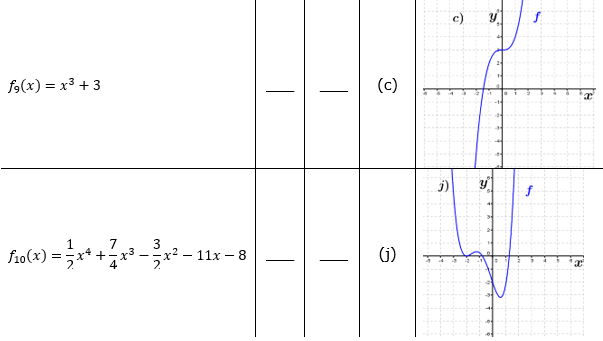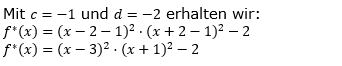 |
Symmetrie ganzrationaler Funktionen - Level 2 - Fortgeschritten - Blatt 3 |
| Dokument mit 19 Aufgaben |
Aufgabe A1 (12 Teilaufgaben)
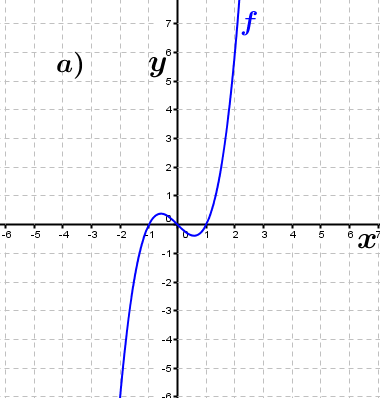
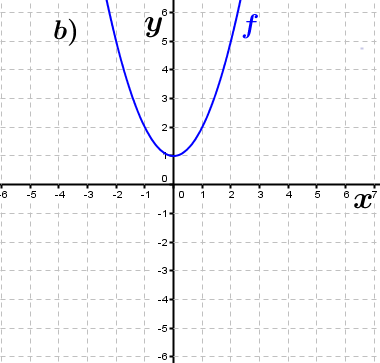
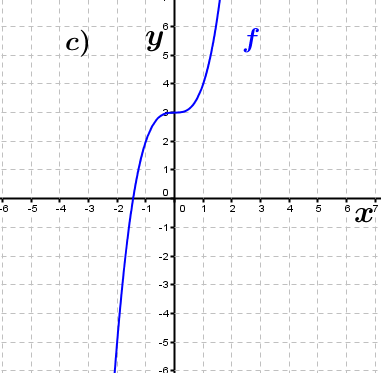
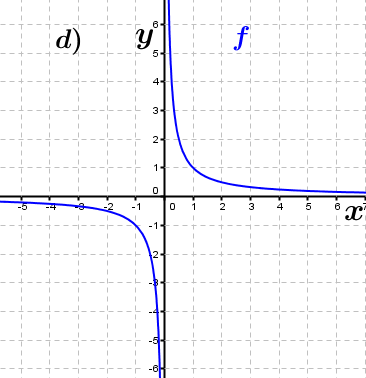
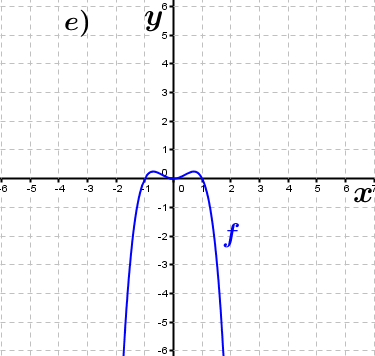
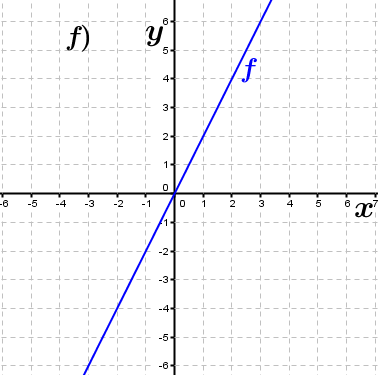
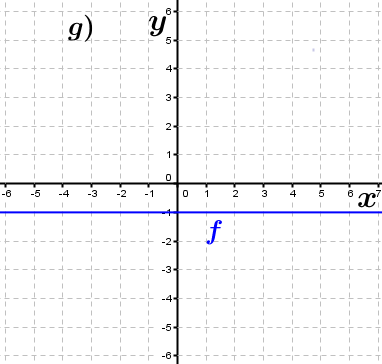
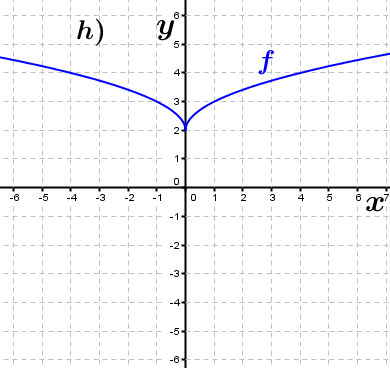
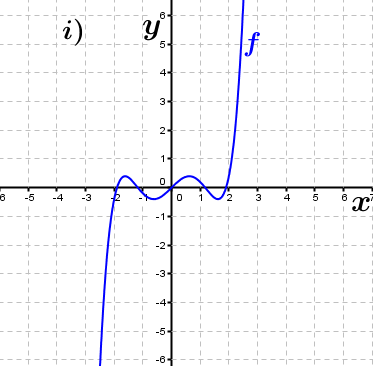
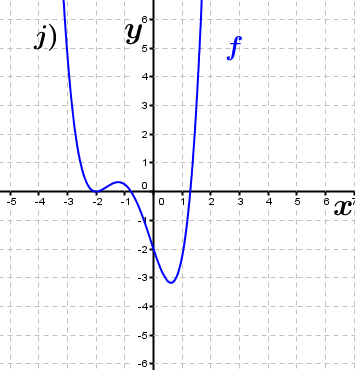
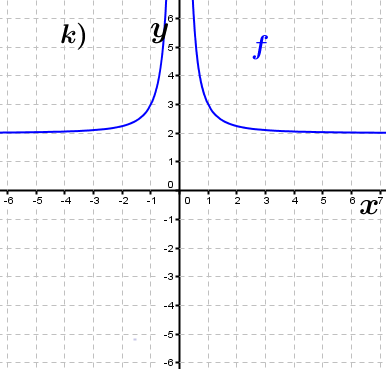
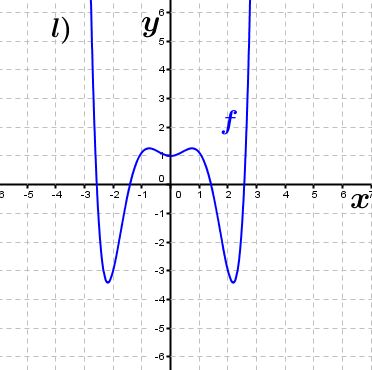
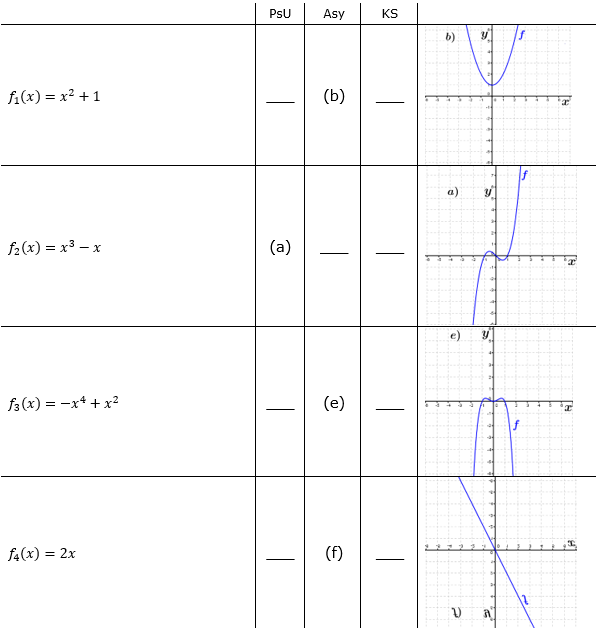
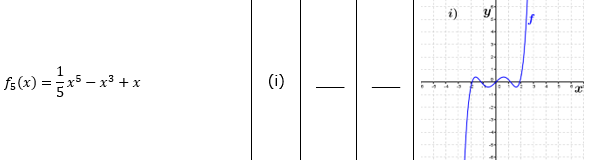
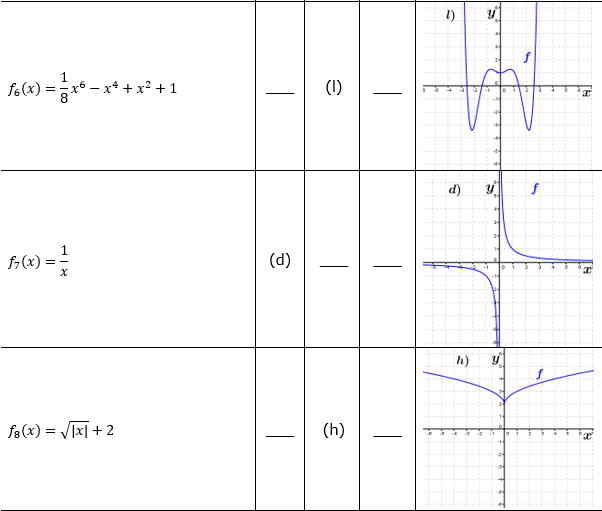
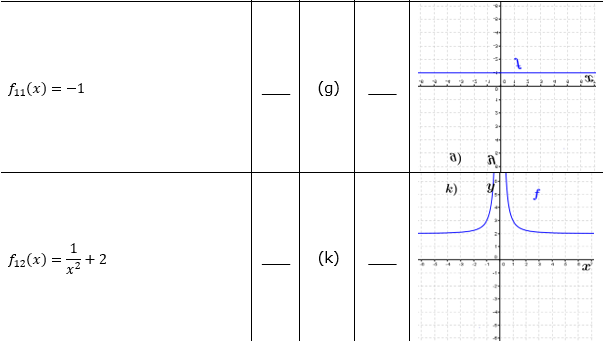
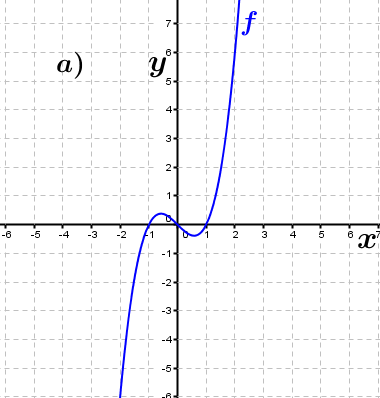
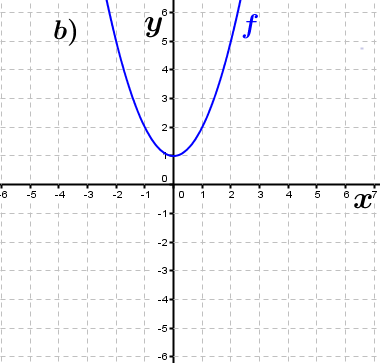
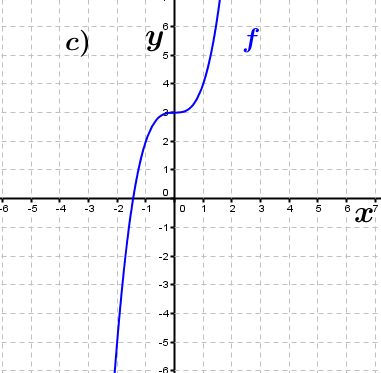
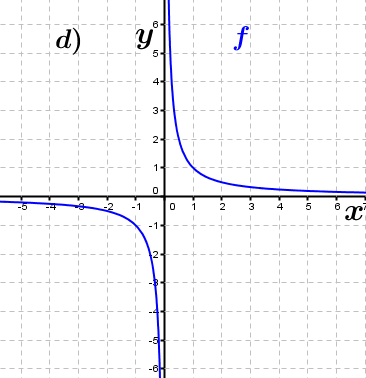
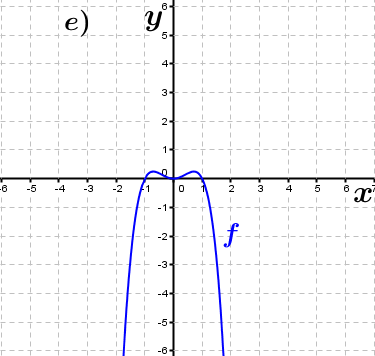
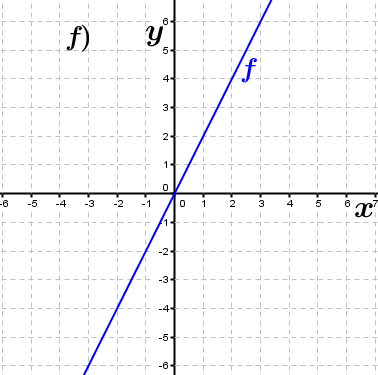
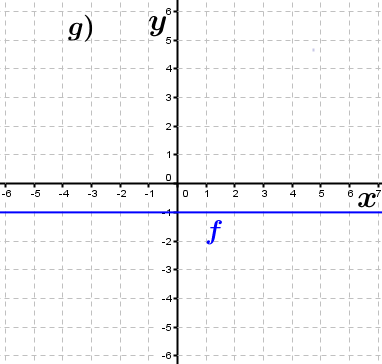
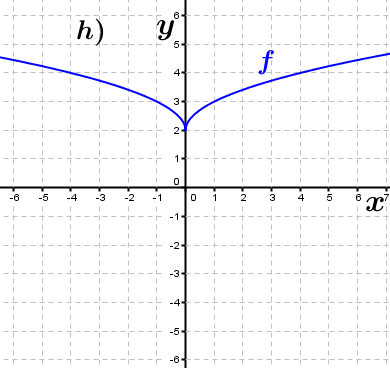
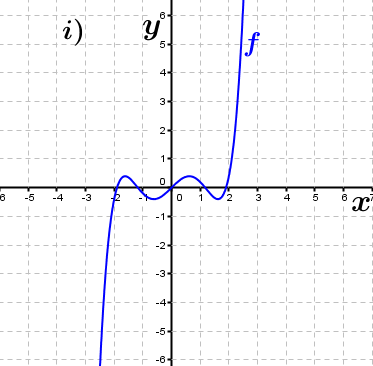
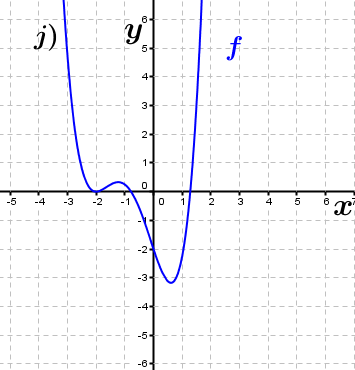
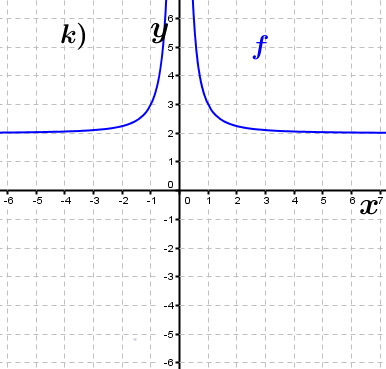
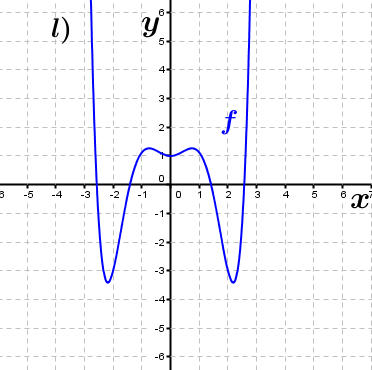
| Bestimme, welcher der nachfolgend abgebildeten Graphen punktsymmetrisch zum Ursprung, achsen-symmetrisch zur y–Achse ist bzw. keine Symmetrie aufweist. Trage deine Lösungen (Buchstaben der Grafik) in die darunter stehende Tabelle ein. Fahre zum Vergrößern der Grafiken mit der Maustaste über die Grafiken. |
|||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Bedeutung der Abkürzungen: PsU = Punktsymmetrisch zum Ursprung, Asy = Achsensymmetrisch zur y–Achse, KS=keine Symmetrie. |
|||
| PsU | Asy | KS | PsU | Asy | KS | ||
| f1(x)=x2+1 | ____ | ____ | ____ | f2(x)=x3-x | ____ | ____ | ____ |
| f3(x)=-x4+x2 | ____ | ____ | ____ | f4(x)=2x | ____ | ____ | ____ |
 |
____ | ____ | ____ |  |
____ | ____ | ____ |
 |
____ | ____ | ____ |  |
____ | ____ | ____ |
 |
____ | ____ | ____ |  |
____ | ____ | ____ |
 |
____ | ____ | ____ |  |
____ | ____ | ____ |
 Eine Frage stellen... |
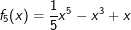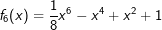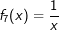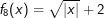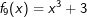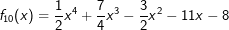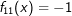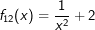Fehler melden...Aufgabe A2 (3 Teilaufgaben)
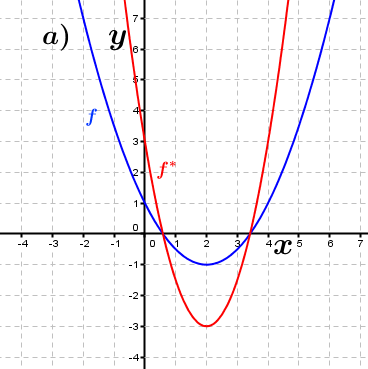
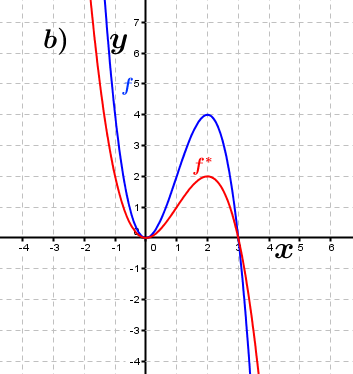
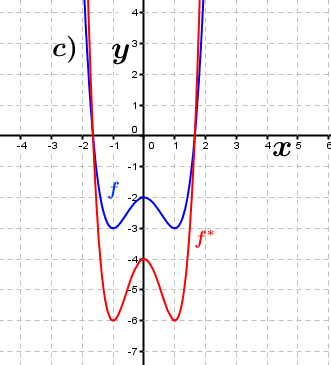
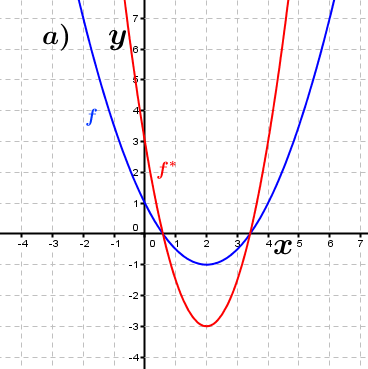
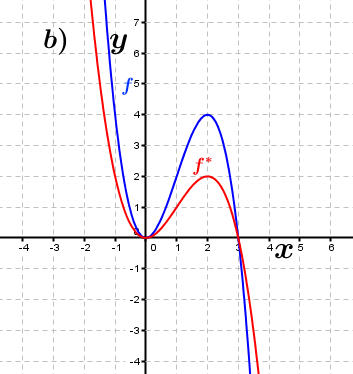
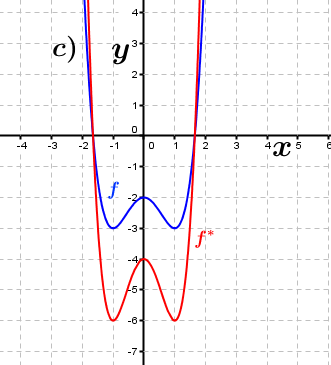
| Bestimme anhand der Graphen, wie groß der jeweilige Streckungsfaktor k in y–Richtung ist, die den Graphen der Funktion f in den Graphen der Funktion f* überführt. Fahre zum Vergrößern der Grafiken mit der Maustaste über die Grafiken. |
||
 |
 |
 |
| Eine Frage stellen... |
Aufgabe A3 (3 Teilaufgaben)
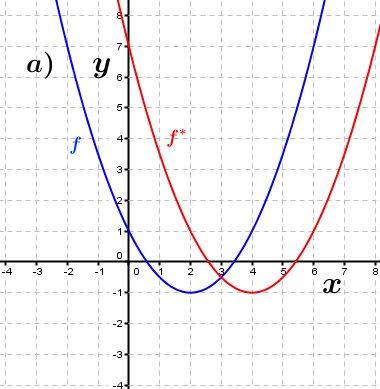
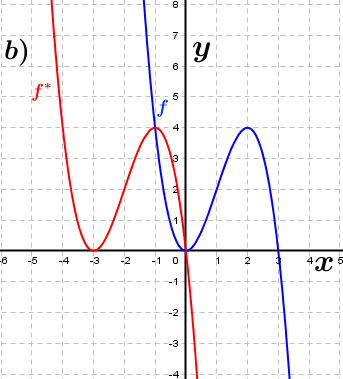
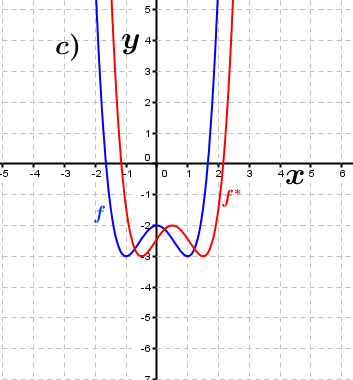
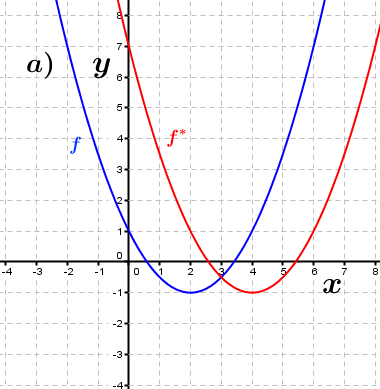
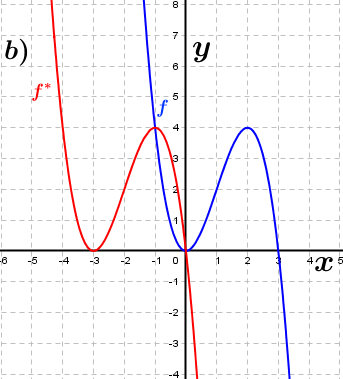
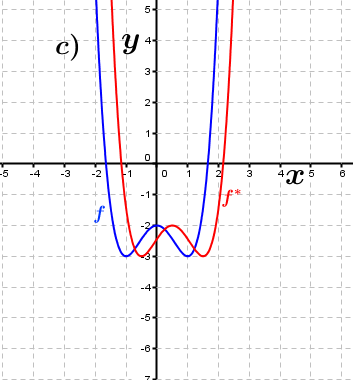
| Bestimme anhand der Graphen, wie groß der jeweilige Verschiebungsfaktor c in x-Richtung ist, der den Graphen der Funktion f in den Graphen der Funktion f* überführt. Fahre zum Vergrößern der Grafiken mit der Maustaste über die Grafiken. |
||
 |
 |
 |
| Eine Frage stellen... |
Aufgabe A4
| Gegeben ist die Funktion f mit f(x)=(x-2)2⋅(x+2)2. Bilde die Funktionsgleichung f*(x) von f*, deren Graph um eine Stelle nach links und zwei Einheiten nach unten verschoben ist. |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Symmetrie ganzrationaler Funktionen - Level 2 - Fortgeschritten - Blatt 3 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
