Quadratische Funktionen (anwendungsorientiert) Level 3 - Expert Aufgabenblatt 2

Dokument mit 9 Aufgaben

Hinweis:
In diesem Aufgabenblatt befinden sich Aufgaben zu anwendungsorientierten Themen.

Aufgabe A1
Lösung A1

Aufgabe A1

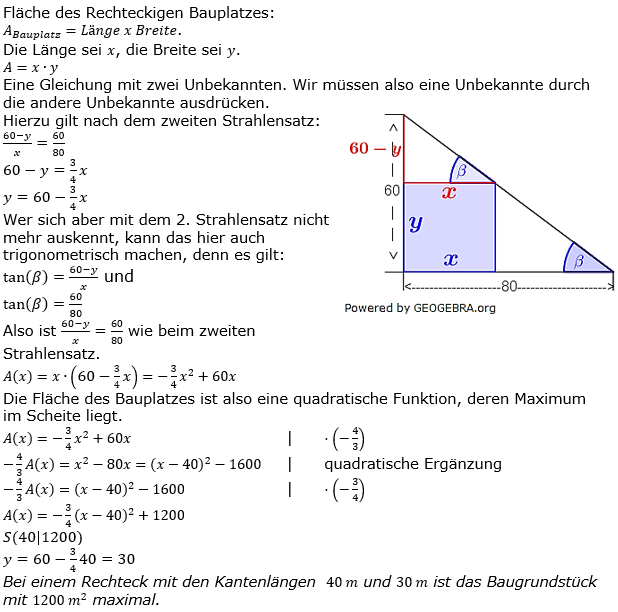
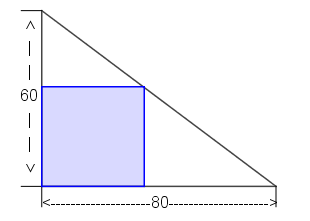Auf einem dreieckigen Grundstück mit den Kantenlängen 60 m und 80 m soll ein möglichst großer rechteckiger Bauplatz abgesteckt werden. (Grafik A320101 im Aufgabensatz 01 Blatt 3/2 Expert zu quadratischen Funktionen (Parabeln) in den Funktionsklassen) /© by www.fit-in-mathe-online.de)

Auf einem dreieckigen Grundstück mit den Kantenlängen 60 m und 80 m soll ein möglichst großer rechteckiger Bauplatz abgesteckt werden. Berechne dessen Seitenlängen a und b.

Aufgabe A2 (4 Teilaufgaben)
Lösung A2

Aufgabe A2 (4 Teilaufgaben)

Ein Eisenbahntunnel hat die Form einer Parabel mit einer Breite von 8 m und einer Höhe von 6 m.

a)	Bestimme eine quadratische Funktion f, deren Graph die Tunneleinfahrt beschreibt.
b)	Zeichne die Tunneleinfahrt im Maßstab 1:100.
c)	Es soll ein neues Zugmodell entwickelt werden, welches den Tunnel durchfahren kann.

Dessen Waggons sind 3,20 m breit und 3,50 m hoch.
Wie weit muss die Schienenmitte vom rechten Tunnelrand für diesen Zug mindestens entfernt sein?

Aufgabe A3
Lösung A3

Aufgabe A3

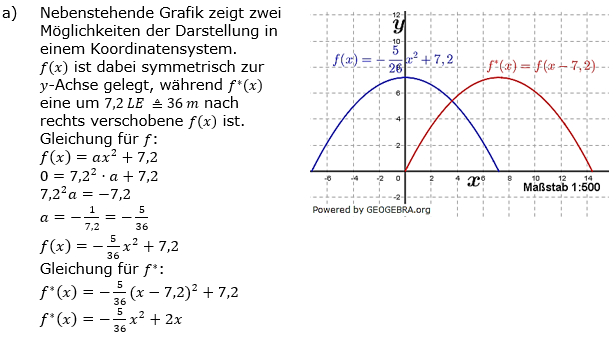
Der Berliner Bogen in Hamburg ist ein Kongress- und Bürozentrum. (Grafik A320301 im Aufgabensatz 03 Blatt 3/2 Expert zu quadratischen Funktionen (Parabeln) in den Funktionsklassen) /© by www.fit-in-mathe-online.de)

Der Berliner Bogen in Hamburg ist ein Kongress- und Bürozentrum. Die Frontansicht ist parabelförmig mit einer Höhe von 36 m und einer Breite von ca. 72 m.

a)	Fertige im Maßstab 1:500 eine Planskizze an. Gib zwei Koordinatensysteme zur Beschreibung der Parabel an und bestimme jeweils den zugehörigen Funktionsterm.

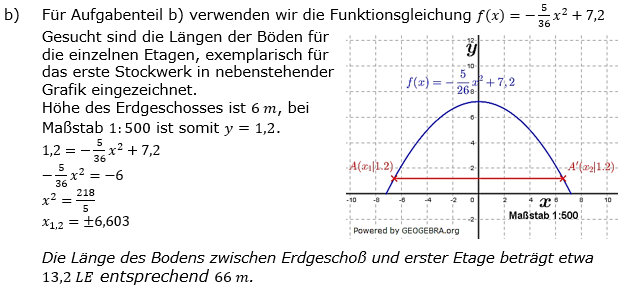
Das Erdgeschoss mit einer Höhe von 6 m ist gefolgt von 6 Stockwerken mit je 4 m Höhe.
Berechne die Gesamtbreite der Böden für die einzelnen Stockwerke.

Aufgabe A4 (2 Teilaufgaben)

Ein Freizeitpark hat bei einem Eintrittspreis von 28 € im Durchschnitt täglich 1600 Besucher. Ein Marktforschungsinstitut ermittelt: Wenn man die Eintrittspreise um 0,50 €, 1,00 €, 1,50 € und 2,00 € usw. senken würde, so stiege die tägliche Besucherzahl um 40, 80, 120, 160 usw. an.
a)	Stelle die täglichen Einnahmen E (in €) in Abhängigkeit von der Preissenkung x (in €) durch eine Funktionsgleichung dar.
b)	Wie hoch sind die täglichen Einnahmen, wenn der Eintrittspreis 22 € beträgt?
c)	Welchen Eintrittspreis müsste der Freizeitpark verlangen, damit die Einnahmen möglichst hoch sind? Wie hoch sind die Einnahmen dann?

Lösungshilfe A4

Wir müssen die Erlösfunktion in Abhängigkeit der Preissenkungen aufstellen.
Bei einem Preis von 28 € kommen täglich 1600 Besucher. Ohne Preissenkung wäre die Erlösfunktion E(x)=28∙1600.
Wird der Preis auf 27,50 € gesenkt kämen Besucher mehr. Die Erlösfunktion wäre:
E(x)=(28-0,5)⋅1600+(28-0,5)⋅40=(28-0,5)⋅(1600+40)
Nun sollen wir das aber aufstellen für Preissenkungen und nicht nur für eine Preissenkung. Damit erhalten wir E(x)=(28-x)∙(1600+40x).

Du befindest dich hier:

Quadratische Funktionen (anwendungsorientiert) Level 3 - Expert - Aufgabenblatt 2

: Geschrieben von Meinolf Müller Meinolf Müller; Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021

Inhalte erstellt

mithilfe von

Joomla! CMS ist freie unter der GNU/GPL-Lizenz veröffentlichte Software und wird verwaltet von einer erstaunlichen Gemeinschaft.

Software-Support

Mit freundlicher Unterstützung

Safi Studio wurde im Jahre 2008 gegründet. Wir erstellen Projekte von höchster Qualität, basierend auf den aktuellsten Web Technologien, innovativ und einzigartig. Über die Jahre haben wir eine große Anzahl Projekte erstellt, die sich erfolgreich im Web platziert haben.

Mathe Grafiken

mithilfe von