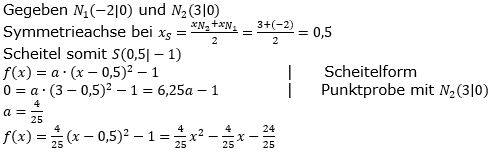 |
Quadratische Funktionen (Parabeln) Level 2 - Fortgeschritten - Aufgabenblatt 1 |
| Dokument mit 26 Aufgaben |
Aufgabe A1 (4 Teilaufgaben)
| Bestimme die Gleichung der Parabel, wenn folgendes bekannt ist: | |
| a) | Die Parabel verläuft durch die Punkte P1 (1|2,5), P2 (-2|1) und P3 (0|3). |
| b) | Für die Funktion f der Parabel gilt f(2)=-1, f(-1)=0,5 und f(4)=3. |
| c) | Die Parabel schneidet die y–Achse in Py(0|4), die x–Achse in N1(-2|0) und die erste Winkelhalbierende in x=2. |
| d) | Die Parabel verläuft durch die Punkte P1(1|-3,5), P2(2|-4) und P3(4|-8). |
 Eine Frage stellen... |
Fehler melden...
Aufgabe A2
| Für eine quadratische f Funktion gilt f(2)=0 und f(0)=4. Welche Eigenschaft hat das Schaubild von f. Bestimmen Sie einen möglichen Funktionsterm. |
| Eine Frage stellen... |
Aufgabe A3 (4 Teilaufgaben)
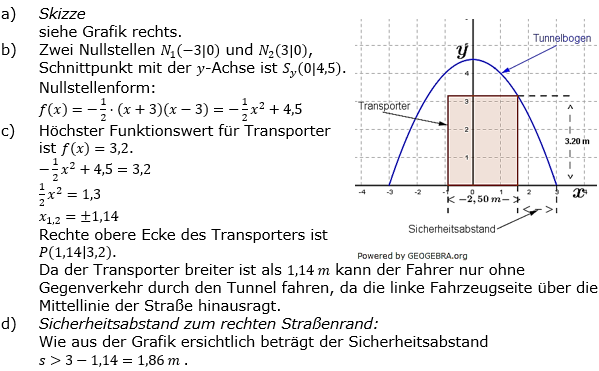
| Ein parabelförmiger Tunnel ist 6 m breit und 4,5 m hoch. Es soll ein 2,5 m breiter Transporter durchfahren. Der Fahrer weiß, dass sein Transporter 3,20 m hoch ist. | |
| a) | Wähle ein geeignetes Koordinatensystem und Skizziere den Tunnel. |
| b) | Bestimme eine passende Funktionsvorschrift, die den Tunnelbogen beschreibt. |
| c) | Wird der Fahrer ohne Gegenverkehr durch den Tunnel fahren können? |
| d) | Welcher Sicherheitsabstand braucht der Fahrer vom rechten Fahrbahnrand? |
| Eine Frage stellen... |
| a) | Wir legen die y-Achse in die „Mitte des Tunnels“ und die x-Achse „auf den Boden“. Die Höhe 4,5 m des Tunnels wird dann zum Scheitelpunkt S(0|4,5) einer nach unten geöffneten Parabel. Die Breite 6 m des Tunnels bestimmt dann die beiden Nullstellen N1 (-3|0) und N2 (3|0). Mit diesen Festlegungen können wir die Form des Tunnels skizzieren. |
| b) | Über die zuvor festgestellten Punkte lässt sich die Parabelgleichung aufstellen. |
| c) | Wir prüfen, ob die rechte obere Ecke des Transporters tiefer ist als die Tunnelwand, wenn der Transporter links mit einen Minimalabstand zur Mittelline (Symmetrieachse) fährt. |
| d) | Der Abstand vom rechten Fahrbahnrand ermittelt sich aus der Hälfte der Fahrbahnbreite und dem rechten Abstand des Transporters zur Fahrbahnmitte so, dass der rechte obere Eckpunkt des Transporters ein Punkt des Parabelbogens ist. |
Aufgabe A4
| Bestimme einen passenden Funktionsterm zu den abgebildeten Parabeln. |
   |
| Eine Frage stellen... |
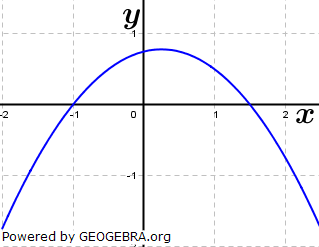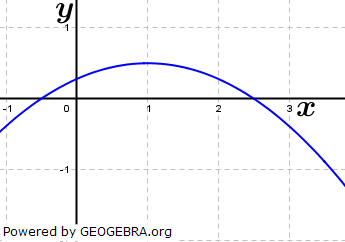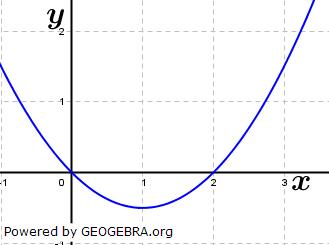Aufgabe A5 (4 Teilaufgaben)
| Der Graph einer quadratischen Funktion geht durch die gegebenen Punkte. Bestimme der Funktionsterm. | |||
| a) | A(-1│2); B(2│1) und C(4│-13) | b) | A(1│5,5); B(-2│-5) und C(3│-5,5) |
| c) | P(1│1); Q(3│0) und R(-2│-1,25) | d) | V(1│1,5); W(-1│-2,5) und T(2│5) |
| Eine Frage stellen... |
Aufgabe A6 (4 Teilaufgaben)
| Der Graph einer quadratischen Funktion f geht durch die angegebenen Punkte. Bestimme den Funktionsterm von f und gib diesen in der Hauptform an. | |||
| a) | Scheitel S(2│7) und A(5│-2) | b) | N1 (2│0); N2 (-1│0) und B(5│-2) |
| c) | Sy (0│2); A(1│3) und B(-1│-3) | d) | Scheitel S(1│-0,5) und Sy (0│-1) |
| Eine Frage stellen... |
Aufgabe A7 (3 Teilaufgaben)
| Bestimme den Funktionsterm einer quadratischen Funktion mit folgenden Eigenschaften: | |
| a) | Der kleinste Funktionswert befindet sich bei x=5 und hat den Wert 0. Bei x=0 ist ihr Wert 2. |
| b) | Der größte Funktionswert befindet sich bei x=-1 und hat den Wert 3. Bei x=1 ist der Wert 1. |
| c) | Die Nullstellen der Funktion befinden sich bei x=5 und x=2. Der größte Funktionswert ist 3. |
| Eine Frage stellen... |
| Aus den Texten heraus müssen wir Bedingungen für das Aufstellen der Funktionsgleichungen herauslesen. | |
| a) | Der Text nennt uns einen Scheitel S(5│0) sowie einen weiteren Punkt P(0│2). |
| b) | Der Text nennt uns einen Scheitel S(-1│3) sowie einen weiteren Punkt P(1│1). |
| c) | Der Text nennt uns zwei Nullstellen N1(5│0) und N2(2│0) sowie den y-Wert des Scheitels S(xS│3). |
Aufgabe A8 (3 Teilaufgaben)
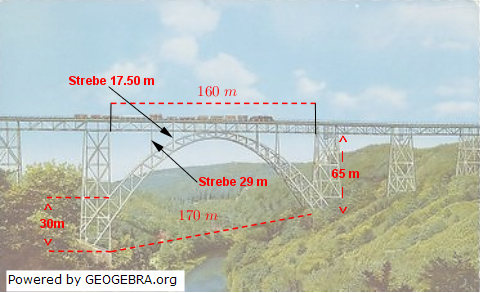
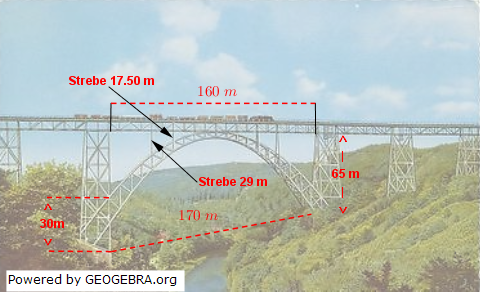 Die höchste Eisenbahnbrücke in Deutschland ist die Münstener Brücke über die Wupper (bei Wuppertal). Die Breite des Bogens am unteren Fuß der Brücke beträgt 170 m, die beiden Pfeiler sind 85 m hoch (siehe Grafik rechts) und 160 m voneinander entfernt. Der obere Parabelbogen hat im Scheitel 5 m Abstand vom unteren Bogen und ist auf 30 m Höhe mit den Pfeilern verschweißt. Je zwei Streben mit 17,5 m und 29 m Länge verbinden die Schienentrasse mit dem unteren Parabelbogen.
 |
|
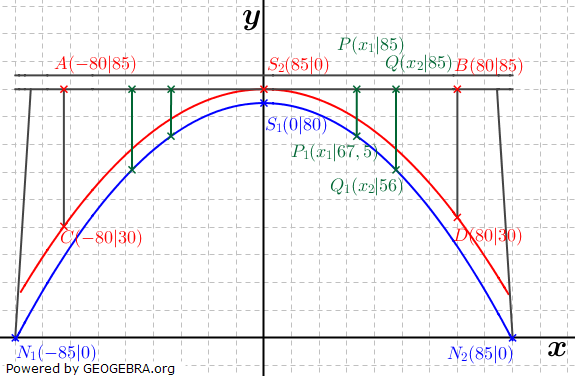
| a) | Wähle ein geeignetes Koordinatensystem und skizziere die beiden Parabelbögen mit den beiden Pfeilern. |
| b) | Bestimme die beiden Funktionsterme. |
| c) | Ermittle die Breite der Parabelbögen an den Stellen, an denen die Streben verankert sind. |
| Eine Frage stellen... |
| a) | Das Koordinatensystem: Wir wählen das Koordinatensystem so, dass der Scheitel des oberen und unteren Parabelbogens der Brücke auf der y-Achse zu liegen kommt. Die x-Achse legen wir in durch die Fußpunkte des rechten und linken Pfeilers. Die Einteilung der Achsen erfolgt in jeweils einer Einheit für 10 m. |
| b) | Aus der Skizze ergeben sich die einzelnen Punkte, gegeben sind jeweils der Scheitelpunkt und ein weiterer Punkt der Parabeln. |
| c) | Für die Breite zwischen den Streben ergeben sich die Fußpunkte der Streben zum unteren Parabelbogen. Wir berechnen dann, an welchen x-Stellen eine der Parabeln den zugehörigen y-Wert besitzt. Über diese Stellen bestimmt sich dann die Breite. |
Aufgabe A9
| Bestimme drei Punkte, durch die man keine Parabel legen kann. Formuliere eine allgemeine Bedingung für die Lage von drei Punkten, sodass es keine Parabel durch diese Punkte gibt. |
| Eine Frage stellen... |
Aufgabe A10
| Eine quadratische Funktion hat die Nullstellen -2 und 3 und den kleinsten Funktionswert -1. Bestimme den Funktionsterm. |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Quadratische Funktionen (Parabel) Level 2 - Fortgeschritten - Aufgabenblatt 1 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 26. September 2022 26. September 2022
