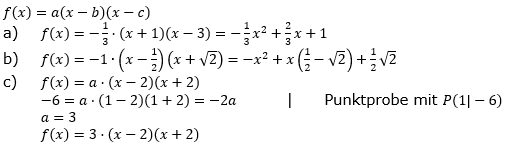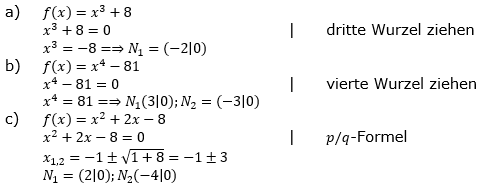|
Nullstellen ganzrationaler Funktionen - Level 2 - Fortgeschritten - Blatt 1 |
| Dokument mit 40 Aufgaben |
Aufgabe A1 (4 Teilaufgaben)
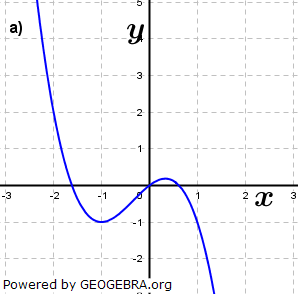
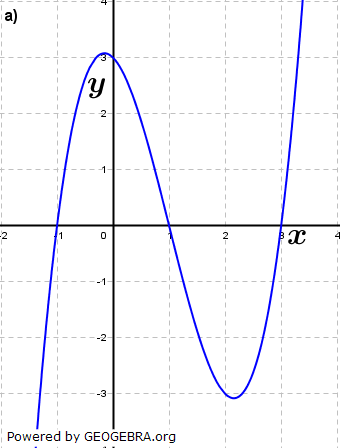
| Ordne den Funktionsgleichungen deren Graphen zu. Begründe deine Entscheidung. | |||
| a) | f(x)=x3-0,5x2-3x+3 | b) | g(x)=-x3-x2+x |
| c) | h(x)=(x-1)(x+2)2 | d) | 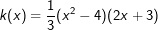 |
 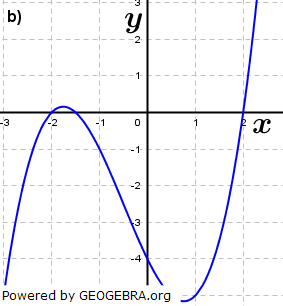 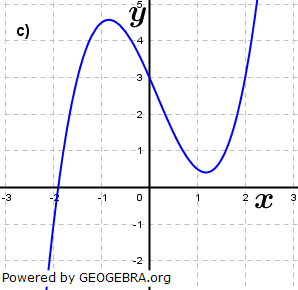 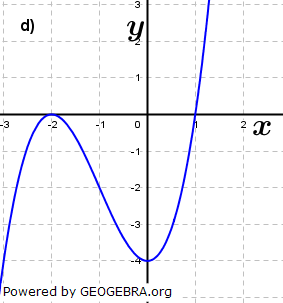 |
|||
| |
Aufgabe A2 (4 Teilaufgaben)
| Ermittle zu den Funktionsgraphen den Funktionsterm. |
 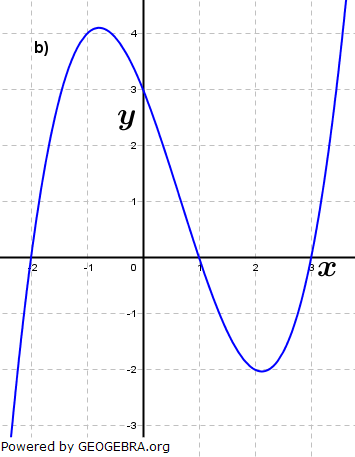 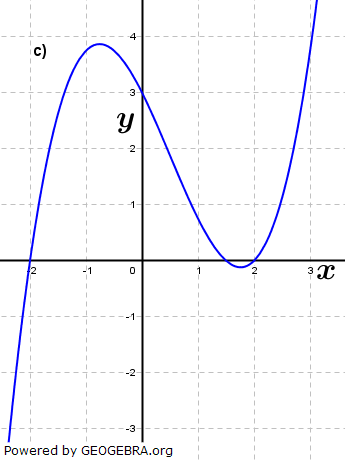 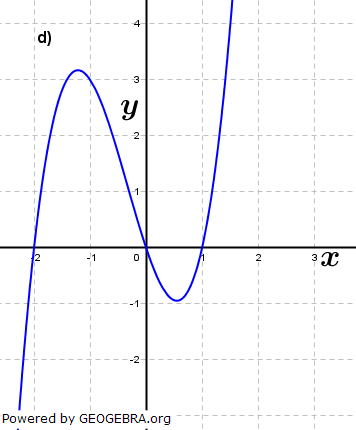 |
| |
Aufgabe A3 (3 Teilaufgaben)
| Wie sind bei der Funktion f mit f(x)=a(x-b)(x-c) die Parameter a, b und c zu wählen, damit f die angegebenen Eigenschaften hat? | |
| a) | Die Nullstellen sind -1 und 3 und der Graph schneidet die y-Achse um Punkt P(0|1). |
| b) | Die Nullstellen sind  und und 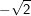 und es gilt f(0)>0. und es gilt f(0)>0. |
| c) | Eine Nullstelle ist -2, der Graph ist achsensymmetrisch zur y-Achse und verläuft durch den Punkt P(1|-6). |
| |
Aufgabe A4 (3 Teilaufgaben)
| Lies die Nullstellen am Graphen ab und bestimme den jeweiligen Grad der Nullstelle. Was lässt sich über den Grad der ganzrationalen Funktion aussagen und welchen Wert besitzt das absolute Glied a0? |
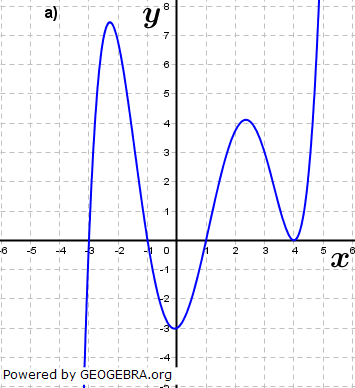 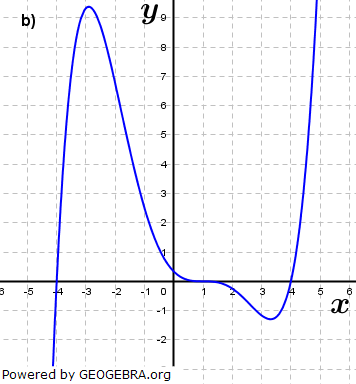 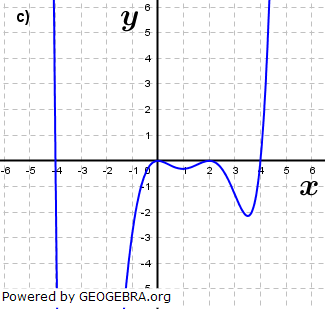 |
| |
Aufgabe A5 (12 Teilaufgaben)
| Nenne das schnellste Verfahren zur Bestimmung der Nullstellen der Graphen der gegebenen Funktionsgleichungen und berechne damit die Nullstelle(n). |
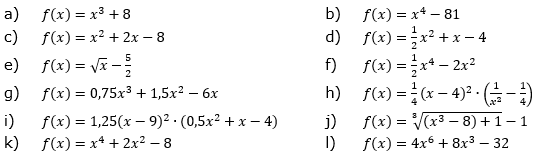 |
| |
Aufgabe A6
Gegeben sei die Funktion f mit  . Vereinfache die Funktionsgleichung soweit wie möglich und gib dann die Nullstellen an. . Vereinfache die Funktionsgleichung soweit wie möglich und gib dann die Nullstellen an. |
| |
Aufgabe A7 (4 Teilaufgaben)
| Beurteile, ob die folgenden Aussagen „immer zutreffen“, „nie zutreffen“ oder „unter bestimmten Bedingungen“ zutreffen. Gib die Bedingung gegebenenfalls an. | |
| a) | Eine ganzrationale Funktion, die ungerade ist, hat mindestens eine Nullstelle. |
| b) | Eine gerade Funktion hat eine gerade Anzahl von Nullstellen. |
| c) | Eine ganzrationale Funktion fünften Grades hat genau 5 Nullstellen. |
| d) | Wenn eine gerade Funktion die Nullstelle 2 besitzt, dann besitzt sie auch die Nullstelle -2. |
| |
Aufgabe A8 (6 Teilaufgaben)
| Berechne die Nullstellen der Funktionen durch Faktorisieren und Verwendung des Satzes vom Nullprodukt. |
 |
| |
Aufgabe A9 (3 Teilaufgaben)
| Untersuche, ob die beschriebene Veränderung des Funktionsterms einer Funktion f die Nullstellen von f verändert. | |
| a) | Der Funktionsterm von f wird mit 2 multipliziert. |
| b) | Zum Funktionsterm von f wird 2 addiert. |
| c) | Der Funktionsterm von f wird quadriert. |
| |
| Du befindest dich hier: |
| Nullstellen ganzrationaler Funktionen - Level 2 - Fortgeschritten - Blatt 1 |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021