|
Potenzfunktionen der Funktionsklassen |


Die Potenzfunktion f(x)=a⋅(x-b)q+c
| Unter Potenzfunktionen verstehen wir Funktionen mit einem einzelnen x-Glied welches eine rationale Potenz aufweist. Die allgemeinen Form einer Potenzfunktion lautet: |
| f(x)=a(x-b)q+c. |
| q ist dabei jede beliebige rationale Zahl, also ganzzahlig positiv, ganzzahlig negativ, oder eine Dezimalzahl bzw. ein endlicher Bruch. |
Auswirkung des Parameters q
Ganzzahlige, positive und gerade Werte von q
| Zunächst betrachten wir uns die einfachste Form einer Potenzfunktion, nämlich f(x)=xq und sehen uns die Bedeutung der Hochzahl q an. | |
Wir betrachten  , also im Bereich der natürlichen Zahlen. , also im Bereich der natürlichen Zahlen.q ist dabei jede beliebige rationale Zahl, also ganzzahlig positiv, ganzzahlig negativ, oder eine Dezimalzahl bzw. ein endlicher Bruch. Die nebenstehende Abbildungen zeigt Graphen von Potenzfunktionen, deren Potenz im angegebenen Bereich liegt. Eine dieser Potenzfunktionen kennen wir schon. |
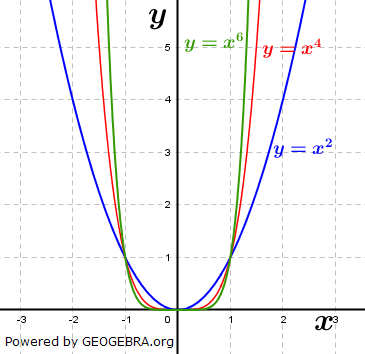 |
| Im Kapitel Quadratische Funktionen / Parabeln haben wir die Funktionsgleichung p(x)=x2, eine Normalparabel, kennengelernt. In der Graphik sehen wir nur geradzahlige Potenzen von x. Je größer die Potenz ist, umso schmäler wird der Graph der Funktion. |
|
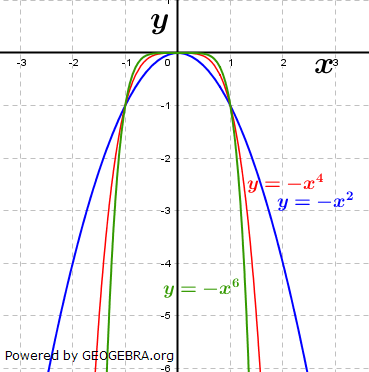
| Ist das Vorzeichen von x ein Minuszeichen, so ist der Graph der Funktion an der x-Achse gespiegelt. Die Auswirkung der geraden Potenz von x ist identisch. Potenzfunktionen mit ganzzahligen geraden Hochzahlen sind achsensymmetrisch zur y-Achse. |
 |
Ganzzahlige, positive und ungerade Werte von q
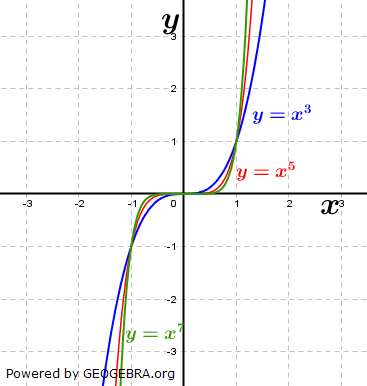
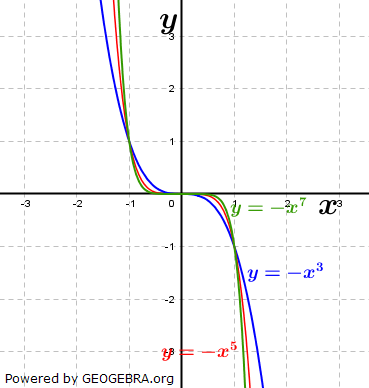
| Sind die ganzzahligen Potenzen von x ungerade, gilt wie bei den geradzahligen Potenzen: Je größer die Potenz ist, umso schmäler wird der Graph der Funktion. Der Graph verläuft aus dem III. Quadranten in den I. Quadranten. |
 |
| Ist das Vorzeichen von x ein Minuszeichen, so ist der Graph der Funktion an der x-Achse gespiegelt. Die Auswirkung der ungeraden Potenz von x ist identisch. Der Graph verläuft aus dem II Quadranten in den IV. Quadranten. Potenzfunktionen mit ganzzahligen ungeraden Hochzahlen sind punktsymmetrisch zu ihrem Wendepunkt. |
 |
Ganzzahlige, negative und gerade Werte von q
| Nachdem wir die Auswirkungen von ganzzahligen positiven Exponenten kennengelernt haben, widmen wir uns den Auswirkungen von ganzzahligen negativen Exponenten. | |
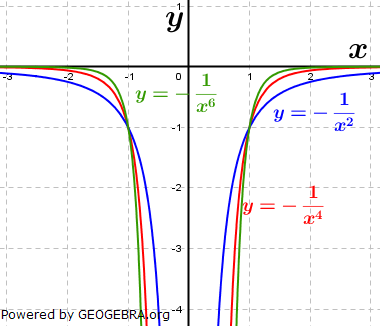
| Wir betrachten zunächst die Exponenten mit geraden negativen Zahlen. Die nebenstehende Grafik zeigt die Schaubilder der Funktionen f, g und h mit f(x)=x-2, g(x)=x-4 und h(x)=x-6. Der aufmerksame Beobachter erkennt, dass in der Grafik eine andere Schreibweise verwendet wurde, nämlich 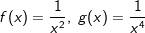 und und 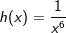 . Hier wurden Potenzgesetze angewandt, nämlich die Umwandlung negativer Hochzahlen in positive Hochzahlen. . Hier wurden Potenzgesetze angewandt, nämlich die Umwandlung negativer Hochzahlen in positive Hochzahlen. |
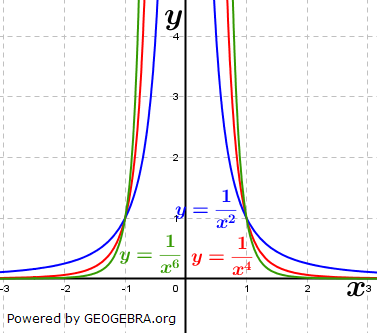 |
| Je größer die Hochzahlen werden, umso steiler wird die Kurve, alle Kurven schneiden sich in den Punkten S1(-1|1) sowie S2(1|1). Die Funktionen sind in x=0 nicht definiert, haben dort eine Definitionslücke. | |
| Ist das Vorzeichen von x ein Minuszeichen, so ist der Graph der Funktion an der x-Achse gespiegelt. Die Auswirkung der geraden Potenzen von x ist identisch. Der Graph verläuft im III. Quadranten in im IV. Quadranten. Potenzfunktionen mit ganzzahligen negativen, geraden Hochzahlen sind achsensymmetrisch zur y-Achse. |
 |
Ganzzahlige, negative und ungerade Werte von q
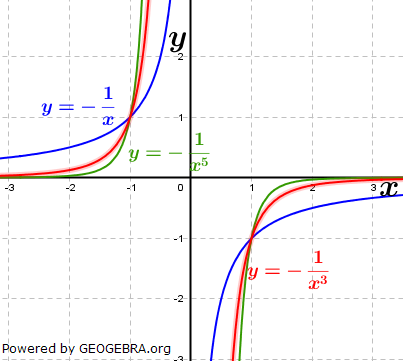
| Wir betrachten jetzt die Exponenten mit ungeraden negativen Zahlen. Die nebenstehende Grafik zeigt die Schaubilder der Funktionen f, g und h mit f(x)=x-1, g(x)=x-3 und h(x)=x-5. Der aufmerksame Beobachter erkennt, dass in der Grafik eine andere Schreibweise verwendet wurde, nämlich 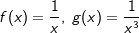 und und 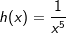 . Hier wurden Potenzgesetze angewandt, nämlich die Umwandlung negativer Hochzahlen in positive Hochzahlen. . Hier wurden Potenzgesetze angewandt, nämlich die Umwandlung negativer Hochzahlen in positive Hochzahlen. |
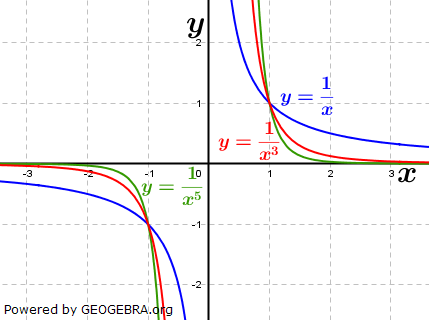 |
| Die Kurve wird umso steiler, je größer die Hochzahlen werden. Alle Kurven schneiden sich in den Punkten S1(-1|-1) sowie S2(1|1). Die Funktionen sind in x=0 nicht definiert, haben dort eine Definitionslücke. | |
| Ist das Vorzeichen von x ein Minuszeichen, so ist der Graph der Funktion an der x-Achse gespiegelt. Die Auswirkung der ungeraden Potenzen von x ist identisch. Der Graph verläuft im II. Quadranten und im IV. Quadranten. Potenzfunktionen mit ganzzahligen negativen, ungeraden Hochzahlen sind punktsymmetrisch zum Ursprung. |
 |
Rationale, positive Werte von q
| Nachdem wir die Auswirkungen von ganzzahligen Exponenten kennengelernt haben, widmen wir uns den Auswirkungen von rationalen sowohl positiven als auch negativen Exponenten. | |
Wir betrachten zunächst die positiven rationalen Zahlen. Die nebenstehende Grafik zeigt die Schaubilder der Funktionen f, g und h mit 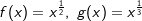 und und 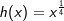 . .Der aufmerksame Beobachter erkennt, dass in der Grafik eine andere Schreibweise verwendet wurde, nämlich 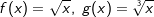 und und 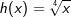 . . |
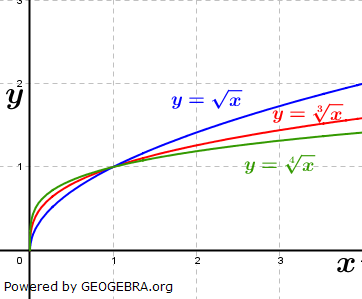 |
| Hier wurden Potenzgesetze angewandt, nämlich die Umwandlung rationaler Hochzahlen in die Wurzelschreibweise. Je kleiner die Hochzahlen werden, umso flacher wird die Kurve. Alle Kurven gehen sowohl durch P(1|1) als auch durch den Ursprung. Sie sind in O(0|0) zwar definiert, sind aber dort nicht differenzierbar. Wir müssen zusätzlich feststellen, dass die Graphen der Funktionen ausschließlich im I. Quadranten verlaufen. Negative Werte von x kommen nicht vor, da negative Zahlen unter Wurzeln nicht zulässig sind. |
|
Allerdings müssen wir hier eine Einschränkung machen, denn wir können diese Funktionen ja an der y-Achse spiegeln. Die nebenstehende Grafik zeigt die Schaubilder der Funktionen f, g und h mit 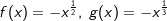 und und 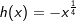 , alle mit , alle mit 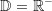 (Definitionsbereich ist der negative reelle Zahlenbereich). (Definitionsbereich ist der negative reelle Zahlenbereich). |
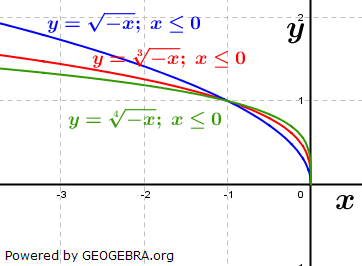 |
Der aufmerksame Beobachter erkennt, dass in der Grafik eine andere Schreibweise verwendet wurde, nämlich 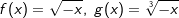 und und 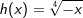 , jeweils aber mit x ≤ 0. Im Übrigen gilt hier das zuvor beschriebene. , jeweils aber mit x ≤ 0. Im Übrigen gilt hier das zuvor beschriebene. |
|
| Ist das Vorzeichen von f(x) ein Minuszeichen, so ist der Graph der Funktion an der x-Achse gespiegelt. Die Auswirkung rationaler Potenzen von x ist identisch mit dem oben Beschriebenen. | 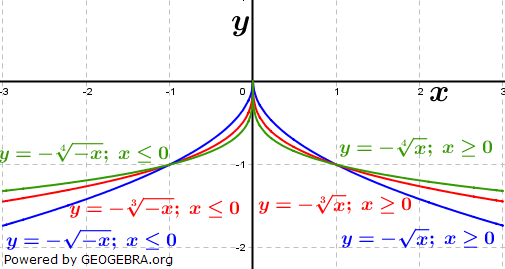 |
| Die Schaubilder der Funktionen mit rationalen positiven Hochzahlen haben einen weiteren Namen, man nennt sie auch Wurzelfunktionen. | |
Rationale, negative Werte von q
Die nebenstehende Grafik zeigt die Schaubilder der Funktionen f, g und h mit rationalem negativem q. Die Funktionsgleichungen lauten: 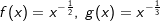 und und 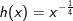 . .Der aufmerksame Beobachter erkennt, dass in der Grafik eine andere Schreibweise verwendet wurde, nämlich 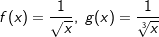 und und 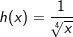 . . |
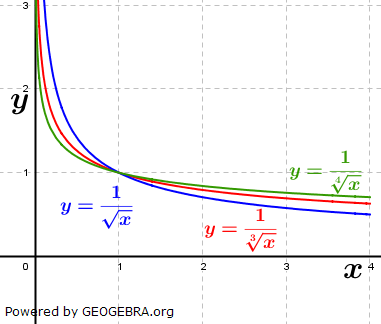 |
| Hier wurden Potenzgesetze angewandt, nämlich zunächst Umwandlung negativer in positive Hochzahlen und dann die Potenzdarstellung von Wurzeln. Je größer die Hochzahlen werden, umso flacher wird die Kurve. Alle Kurven gehen durch P(1|1). Die Funktionen sind für x=0 nicht definiert. Im Übrigen gilt das unter ganzzahlig negativen Werten von q Beschriebene. |
|
| Auch diese Funktionen können an der y-Achse gespiegelt werden. Es gilt das unter „Auswirkung rationaler positiver Werte von q„ Beschriebene analog. | 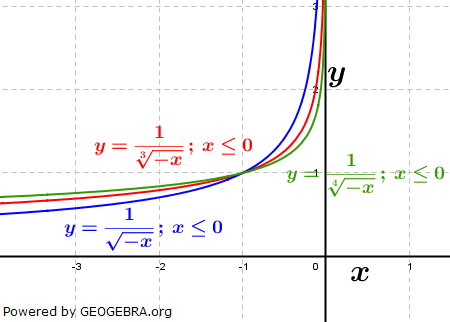 |
| Ist das Vorzeichen von f(x) ein Minuszeichen, so ist der Graph der Funktion an der x-Achse gespiegelt. Es gilt das unter „Auswirkung rationaler positiver Werte von q“ bereits Angeführte analog. | 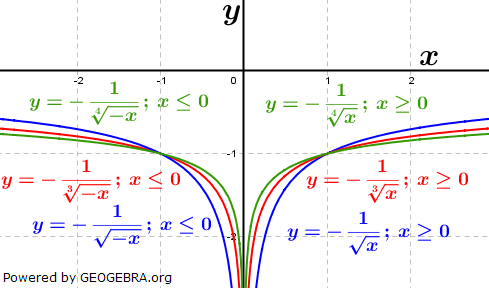 |
Auswirkung des Parameters b
| Der Parameter b beeinflusst die Verschiebung des Graphen der Funktion in x-Richtung. | |
| Für den Parameter b gilt: Ist b positiv, wird der Graph in x-Richtung um die Anzahl Einheiten nach rechts verschoben, die durch den Wert von b angegeben ist. Ist b negativ, wird der Graph in x-Richtung um die Anzahl Einheiten nach links verschoben, die durch den Wert von b angegeben ist. Die nebenstehende Animation verdeutlicht dies an Hand der Funktionsgleichung f(x)=(x-b)3. |
|
| Die Animation kann durch einen Klick auf "Start" gestartet werden, ein Klick auf "Pause" hält die Animation an, ein Klick auf "Stop" zeigt wieder die Ausgangsstellung. Zunächst läuft der Parameter a von -3 bis +3. Danach läuft für a=1 der Parameter b von 0 bis +3 und dann von -3 bis 0. |
|
| Hinweis: Ist b positiv, muss in der Funktionsgleichung (x-b)q angegeben werden. Ist b negativ, muss in der Funktionsgleichung (x+b)q angegeben werden. |
|
Auswirkung des Parameters c
| Der Parameter c beeinflusst die Verschiebung des Graphen der Funktion in y-Richtung. | |
| Für den Parameter c gilt: Ist c positiv, wird der Graph in y-Richtung um die Anzahl Einheiten nach oben verschoben, die durch den Wert von c angegeben ist. Ist c negativ, wird der Graph in c-Richtung um die Anzahl Einheiten nach unten verschoben, die durch den Wert von c angegeben ist. Die nebenstehende Animation verdeutlicht dies an Hand der Funktionsgleichung f(x)=a⋅x4+c. |
|
| Die Animation kann durch einen Klick auf "Start" gestartet werden, ein Klick auf "Pause" hält die Animation an, ein Klick auf "Stop" zeigt wieder die Ausgangsstellung. Zunächst läuft der Parameter a von -3 bis +3. Danach läuft für a=1 der Parameter c von 0 bis +3 und dann von -3 bis 0. |
|
Definitions- und Wertebereich von Potenzfunktionen
| Definitions- und Wertebereich (auch Definitionsmenge bzw. Wertemenge genannt) von Funktionen bestimmen den Verlauf des Graphen einer Funktion, so auch bei den Potenzfunktionen. Zur Erinnerung hier noch einmal die Definition der beiden Bereiche: |
Definitionsbereich (Definitionsmenge)
Der Definitionsbereich umfasst alle für eine Funktion gültigen x-Werte. Er wird mit 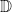 bzw. einfach nur D bezeichnet. bzw. einfach nur D bezeichnet. |
Wertebereich (Wertemenge)
Der Wertebereich umfasst alle für eine Funktion sich aus den gültigen x-Werten ergebende y-Werte. Er wird mit 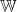 bzw. einfach nur W bezeichnet. bzw. einfach nur W bezeichnet. |
Beispiele
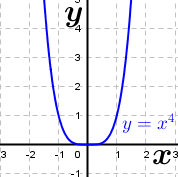
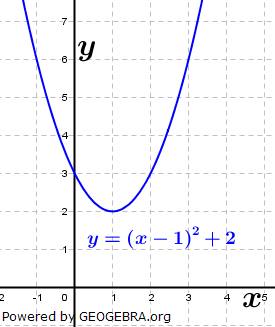 Die gegebene Funktion ist eine Potenzfunktion 2. Grades (Parabel). Aus dem nebenstehenden Graphen erkennen wir, dass alle reellen Zahlen der Variablen x zugeordnet werden können, da sich für jedes beliebige x ein ganz bestimmter Funktionswert f(x)=y ergibt. Wir schreiben: Die gegebene Funktion ist eine Potenzfunktion 2. Grades (Parabel). Aus dem nebenstehenden Graphen erkennen wir, dass alle reellen Zahlen der Variablen x zugeordnet werden können, da sich für jedes beliebige x ein ganz bestimmter Funktionswert f(x)=y ergibt. Wir schreiben: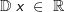 (sprich Definitionsbereich ist die (sprich Definitionsbereich ist dieMenge der reellen Zahlen) Anders ist dies beim Wertebereich. Der tiefste Punkt des Graphen der Funktion hat den y-Wert f(x)=2. Kleinere y-Werte können nicht vorkommen. Wir schreiben: 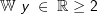 (sprich der Wertebereich ist die Teilmenge der reellen Zahlen (sprich der Wertebereich ist die Teilmenge der reellen Zahlengrößer oder gleich zwei). |
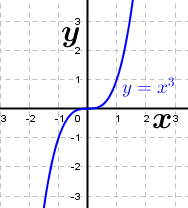
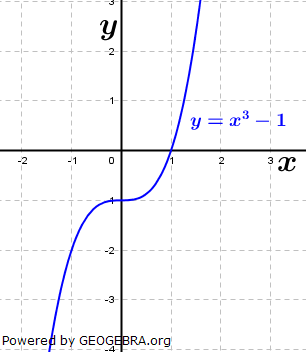 Die gegebene Funktion ist eine Potenzfunktion 3. Grades. Aus dem nebenstehenden Graphen erkennen wir, dass alle reellen Zahlen der Variablen x zugeordnet werden können, da sich für jedes beliebige x ein ganz bestimmter Funktionswert f(x)=y ergibt. Wir schreiben: Die gegebene Funktion ist eine Potenzfunktion 3. Grades. Aus dem nebenstehenden Graphen erkennen wir, dass alle reellen Zahlen der Variablen x zugeordnet werden können, da sich für jedes beliebige x ein ganz bestimmter Funktionswert f(x)=y ergibt. Wir schreiben: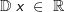 (sprich Definitionsbereich ist die (sprich Definitionsbereich ist dieMenge der reellen Zahlen) Da der Graph der Funktion aus dem III. Quadranten in den I. Quadranten verläuft, gilt dies entsprechend auch für den Wertbereich. Wir schreiben: 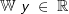 (sprich der Wertebereich ist die Menge der reellen Zahlen). (sprich der Wertebereich ist die Menge der reellen Zahlen). |
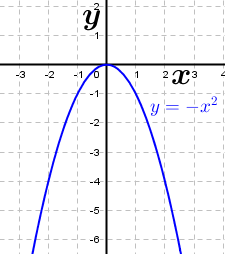
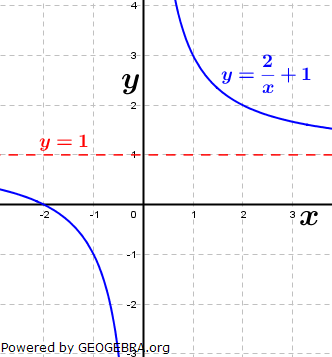 Die gegebene Funktion ist eine Potenzfunktion mit negativem Exponenten Die gegebene Funktion ist eine Potenzfunktion mit negativem Exponenten 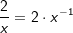 . Aus dem nebenstehenden Graphen erkennen wir, dass mit einer einzigen Ausnahme alle reellen Zahlen der Variablen x zugeordnet werden können, da sich für jedes beliebige x ein ganz bestimmter Funktionswert f(x)=y ergibt. Die Ausnahme ist bei x=0, denn dadurch wird ja der Nenner von f zu Null, was einer besonderen Betrachtung bedarf. Wir schreiben: . Aus dem nebenstehenden Graphen erkennen wir, dass mit einer einzigen Ausnahme alle reellen Zahlen der Variablen x zugeordnet werden können, da sich für jedes beliebige x ein ganz bestimmter Funktionswert f(x)=y ergibt. Die Ausnahme ist bei x=0, denn dadurch wird ja der Nenner von f zu Null, was einer besonderen Betrachtung bedarf. Wir schreiben: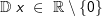 (sprich Definitionsbereich ist die Menge der reellen (sprich Definitionsbereich ist die Menge der reellenZahlen mit Ausnahme von 0) Für den Wertebereich ergibt sich auch eine Ausnahme, in obiger Grafik durch die Parallele zur x-Achse mit y=1 gekennzeichnet. Für x→±∞ läuft 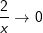 . Da jedoch . Da jedoch 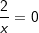 nie erreicht wird, kann die Funktion nie den Wert 1 annehmen. Wir schreiben: nie erreicht wird, kann die Funktion nie den Wert 1 annehmen. Wir schreiben: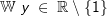 (sprich der Wertebereich ist die Menge der reellen (sprich der Wertebereich ist die Menge der reellenZahlen mit Ausnahme von 1). |
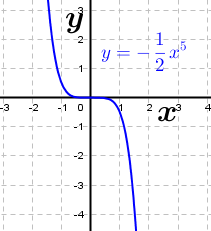
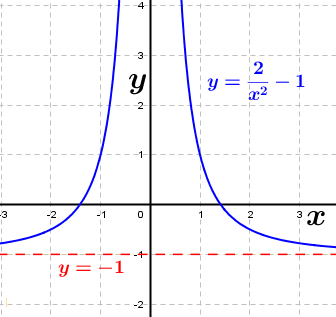 Die gegebene Funktion ist eine Potenzfunktion mit negativem Exponenten Die gegebene Funktion ist eine Potenzfunktion mit negativem Exponenten 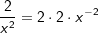 .Aus dem nebenstehenden Graphen erkennen wir, dass mit einer einzigen Ausnahme alle reellen Zahlen der Variablen x zugeordnet werden können, da sich für jedes beliebige x ein ganz bestimmter Funktionswert f(x)=y ergibt. Die Ausnahme ist bei x=0, denn dadurch wird ja der Nenner von f zu Null, was einer besonderen Betrachtung bedarf. Wir schreiben: .Aus dem nebenstehenden Graphen erkennen wir, dass mit einer einzigen Ausnahme alle reellen Zahlen der Variablen x zugeordnet werden können, da sich für jedes beliebige x ein ganz bestimmter Funktionswert f(x)=y ergibt. Die Ausnahme ist bei x=0, denn dadurch wird ja der Nenner von f zu Null, was einer besonderen Betrachtung bedarf. Wir schreiben: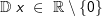 (sprich Definitionsbereich ist die Menge der reellen (sprich Definitionsbereich ist die Menge der reellenZahlen mit Ausnahme von 0) Für den Wertebereich ergibt sich auch eine Ausnahme, in obiger Grafik durch die Parallele zur x-Achse mit y=-1 gekennzeichnet. Für x→±∞ läuft 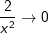 . Da jedoch . Da jedoch 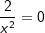 nie erreicht wird, kann die Funktion nie den Wert -1 annehmen. Wir schreiben: nie erreicht wird, kann die Funktion nie den Wert -1 annehmen. Wir schreiben: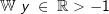 (sprich der Wertebereich ist die Teilmenge der reellen (sprich der Wertebereich ist die Teilmenge der reellenZahlen größer als -1). |
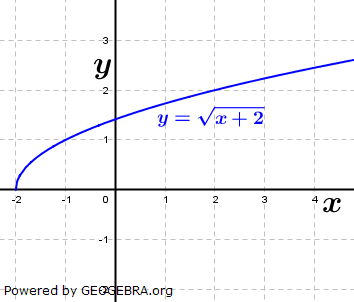 Die gegebene Funktion ist eine Potenzfunktion mit rationalem Exponenten ( Die gegebene Funktion ist eine Potenzfunktion mit rationalem Exponenten (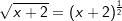 ). Aus dem nebenstehenden Graphen als auch aus dem Term unter der Wurzel erkennen wir, dass x-Werte kleiner als -2 nicht eingesetzt werden können, da sich für x<-2 ein negativer Wert unter der Wurzel ergibt. Wir schreiben: ). Aus dem nebenstehenden Graphen als auch aus dem Term unter der Wurzel erkennen wir, dass x-Werte kleiner als -2 nicht eingesetzt werden können, da sich für x<-2 ein negativer Wert unter der Wurzel ergibt. Wir schreiben: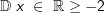 (sprich Definitionsbereich ist (sprich Definitionsbereich istdie Teilmenge der reellen Zahlen größer gleich -2) Für den Wertebereich erkennen wir ebenfalls aus der Grafik als auch aus der Funktionsgleichung, dass y-Werte kleiner als 0 nicht vorkommen können. Wir schreiben: 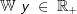 (sprich der Wertebereich ist die Teilmenge der positiven (sprich der Wertebereich ist die Teilmenge der positivenreellen Zahlen einschließlich der 0). |
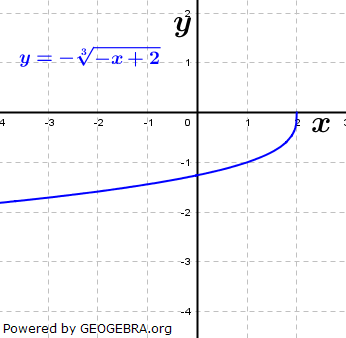 Die gegebene Funktion ist eine Potenzfunktion mit rationalem Exponenten Die gegebene Funktion ist eine Potenzfunktion mit rationalem Exponenten ( 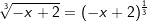 ). Aus dem nebenstehenden Graphen als auch aus dem Term unter der Wurzel erkennen wir, dass x-Werte größer als 2 nicht eingesetzt werden können, da sich für x>2 ein negativer Wert unter der Wurzel ergibt. Wir schreiben: ). Aus dem nebenstehenden Graphen als auch aus dem Term unter der Wurzel erkennen wir, dass x-Werte größer als 2 nicht eingesetzt werden können, da sich für x>2 ein negativer Wert unter der Wurzel ergibt. Wir schreiben: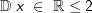 (sprich Definitionsbereich ist (sprich Definitionsbereich istdie Teilmenge der reellen Zahlen kleiner gleich 2) Für den Wertebereich erkennen wir ebenfalls aus der Grafik als auch aus der Funktionsgleichung, dass y-Werte größer als 0 nicht vorkommen können. Wir schreiben: 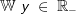 (sprich der Wertebereich ist die Teilmenge der negativen (sprich der Wertebereich ist die Teilmenge der negativenreellen Zahlen einschließlich der 0). |
Symmetrien von Potenzfunktionen
| Auch Potenzfunktionen haben ein Symmetrieverhalten. Die nachfolgende Übersicht zeigt dir, bei welcher Art von Potenzfunktion welche Symmetrie vorliegt. Detaillierte Information über Symmetrien findest du im Kapitel |
| „Graphen und Funktionen analysieren“ |
| hier im Portal. Symmetrien der Funktion f mit 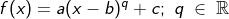 . . |
| Titel Aufgabenblatt | Level / Blattnr. |
Potenzfunktionen Aufgabenblatt Level 1 / Blatt 1  27 Aufgaben im Blatt |
Potenzfunktionen Aufgabenblatt Level 1 / Blatt 2 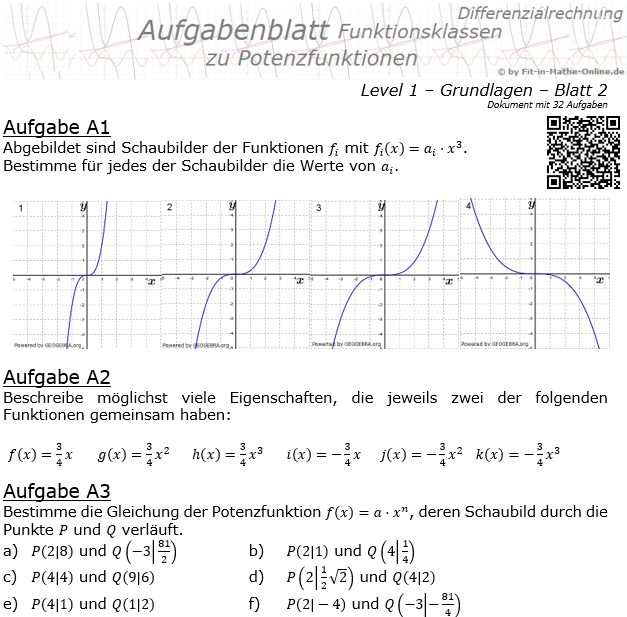 32 Aufgaben im Blatt |
Potenzfunktionen Aufgabenblatt Level 2 / Blatt 1  41 Aufgaben im Blatt |
Potenzfunktionen Aufgabenblatt Level 2 / Blatt 2  23 Aufgaben im Blatt |
Potenzfunktionen Aufgabenblatt Level 3 / Blatt 1  25 Aufgaben im Blatt |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 19. Juli 2021 19. Juli 2021

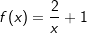 . Bestimme Definitions- und Wertbereich.
. Bestimme Definitions- und Wertbereich.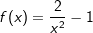 . Bestimme Definitions- und Wertbereich.
. Bestimme Definitions- und Wertbereich.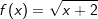 . Bestimme Definitions- und Wertbereich.
. Bestimme Definitions- und Wertbereich.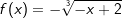 . Bestimme Definitions- und Wertbereich.
. Bestimme Definitions- und Wertbereich. und
und