 |
Ganzrationale Funktionen der Funktionsklassen |
Vielfachheit von Nullstellen
| Wir betrachten in diesem Abschnitt die Mehrfachheit von Nullstellen, die wir zwar bereits früher kennengelernt haben, ohne etwas über diese Mehrfachheit zu wissen. Liegt die Funktionsgleichung einer ganzrationalen Funktion in Produktdarstellung (→ Linearfaktorzerlegung) vor, können wir anhand des Funktionsterms Aussagen über das Verhalten in der Umgebung der Nullstellen machen. Von besonderem Interesse sind dabei mehrfach auftretende Faktoren. Hierzu betrachten wir uns drei Beispiele. |
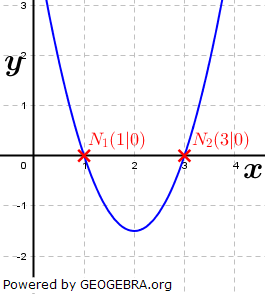
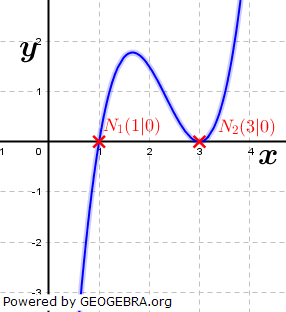
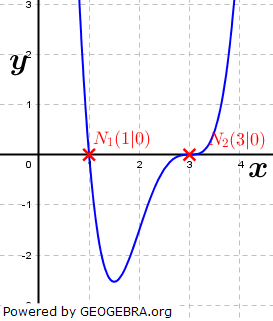
| f(x)=1,5x2-6x+3 | g(x)=1,5x3-10,5x2+22,5x-13,5 | h(x)=1,5x4-15x3+54x2-81x+40,5 |
| f(x)=1,5(x-1)(x-3) | g(x)=1,5(x-1) (x-3)2 | h(x)=1,5(x-1) (x-3)3 |
 |
 |
 |
| Vergleichen wir die oben dargestellten Graphen der jeweiligen Funktionen f, g und h, so stellen wir Folgendes fest: An der Stelle x=1 schneiden alle drei Graphen die x-Achse wie eine Gerade. An der Stelle x=3 schneidet der Graph von f die x-Achse wie eine Gerade, der Graph von g berührt die x-Achse (ähnlich dem Scheitelpunkt einer Parabel) und der Graph von h schneidet die x-Achse ähnlich der Nullstelle einer Funktion i mit i(x)=x3 an der Stelle x=0. |
||
| Das Verhalten der drei Graphen an der Stelle x=3 wird also vom jeweiligen Funktionsglied (x-3) der Funktionsgleichungen bestimmt. Im Falle des Graphen von f hat das Funktionsglied (x-3)1 die Potenz 1. Im Falle des Graphen von g hat das Funktionsglied (x-3)2 die Potenz 2. Im Falle des Graphen von h hat das Funktionsglied (x-3)3 die Potenz 3. |
||
| Das Verhalten der Funktionen in der Umgebung der Nullstelle x=3 wird also von der Vielfachheit des Faktors (x-3) der Produktdarstellung bestimmt. Wir veranschaulichen uns dieses Verhalten für eine ganzrationale Funktion dritten Grades in nebenstehender Animation: | |
| Die Animation kann durch einen Klick auf "Start" gestartet werden, Klick auf "Pause" hält die Animation an, Klick auf "Weiter" setzt sie fort und ein Klick auf "Stop" zeigt wieder die Ausgangsstellung. Für eine Funktionen g mit g(x)=1,5(x-1)(x-3)(x-5) bewegt sich die Nullstelle bei x3=5 schrittweise auf die Nullstelle x2=3 zu. Wird letztendlich x3 zu x2, so fallen die beiden Nullstellen zusammen. Dadurch berührt der Graph die x-Achse an der Stelle x2=3 und die Funktionsgleichung lautet g(x)=1,5(x-1)(x-3)2. Die einfache Nullstelle bei x3=5 wird zur doppelten Nullstelle bei x2=3. |
|
| In diesem Falle sprechen wir bei x2=3 von einer zweifachen (oder auch doppelten) Nullstelle. Die Nullstelle x1=1 hingegen wird einfache Nullstelle genannt. Dies führt uns zu folgendem | |
|
Merksatz Vielfachheit von Nullstellen
|
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
