 |
Ganzrationale Funktionen anwendungsorientiert - Level 3 - Expert - Blatt 4 |
| Dokument mit 14 Aufgaben |
Aufgabe A1 (2 Teilaufgaben)
| Die symmetrische Querschnittsfläche eines Gebirgstales lässt sich durch eine ganzrationale Funktion 4. Grades beschreiben. | ||
| Berechne für verschiedene Windgeschwindigkeiten bis 20 m/s die Leistung der Anlage. |  |
|
| a) | Bestimme den Funktionsterm. | |
| b) | Ein 250 m hoher Staudamm soll errichtet werden. Wie breit ist die Dammkrone (auf eine Dezimale gerundet)? | |
 Eine Frage stellen... |
Fehler melden...Aufgabe A2 (3 Teilaufgaben)
| Ein 100-m-Sprint lässt sich durch eine Polynomfunktion 3. Grades beschreiben. | ||
| a) | Bestätige, dass die nebenstehende Abbildung das Schaubild von f mit  zeigt. Wähle eine geeignete Achseneinteilung. |
 |
| b) | Bestimme die Laufzeit für 100 m auf eine Zehntelsekunde genau. | |
| c) | Bestimme die mittlere Geschwindigkeit des Läufers. | |
| Eine Frage stellen... |
Aufgabe A3 (3 Teilaufgaben)
| Ein Zug bewegt sich nach folgendem Weg-Zeit-Gesetz: | ||
 (t in h, s in km) |
||
| a) | Zeichne das Schaubild der Funktion s(t). Interpretiere den Verlauf. | |
| b) | Bestimme die maximale Entfernung des Zuges vom Ausgangspunkt. | |
| c) | Berechne die mittlere Geschwindigkeit des Zuges im Zeitintervall [0;2]. | |
| Eine Frage stellen... |
Aufgabe A4 (4 Teilaufgaben)
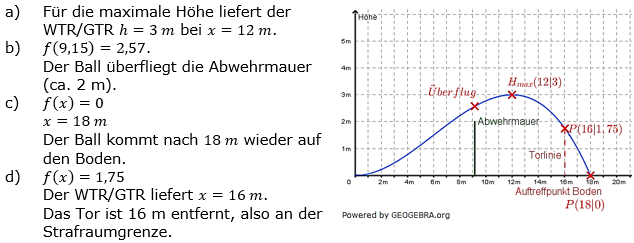
Der Graph der Funktion f mit  ist näherungsweise die Flugkurve des Balles bei einem Freistoß in einem Fußballspiel. |
||
| a) | Skizziere das Schaubild von f. Welche maximale Höhe erreicht der Ball? | |
| b) | Überfliegt der Ball die Abwehrmauer in 9,15 m Entfernung? | |
| c) | Wo kommt der Ball wieder auf den Boden? | |
| d) | Wie weit entfernt vom Tor wurde der direkte Freistoß ausgeführt, wenn der Ball in einer Höhe von 1,75 m die Torlinie überschreitet? | |
| Eine Frage stellen... |
Aufgabe A5 (2 Teilaufgaben)
| Ein Hundehalter plaudert auf dem Feld mit einem Bauer. Sein Hund rennt ihm weg. Das Diagramm zeigt die Geschwindigkeit v (in m/s) des Hundes. | ||
| a) | Interpretiere das Diagramm. |  |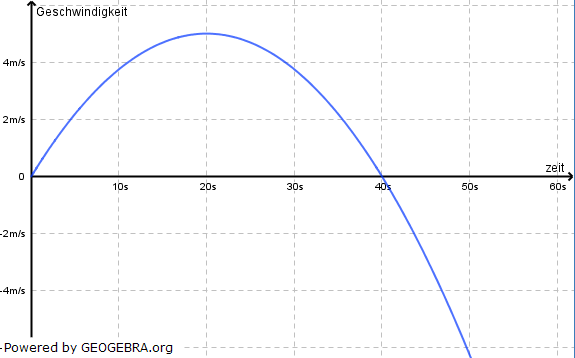
| b) | Gib den Funktionsterm der Geschwindigkeit-Zeit-Funktion v in Abhängigkeit von t an. | |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Ganzrationale Funktionen anwendungsorientiert - Level 3 - Expert - Blatt 4 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
