 Wir betrachten nun eine Funktion mit n=3. Wir betrachten nun eine Funktion mit n=3.
Der Graph der rechts dargestellten Funktion hat die Funktionsgleichung f(x)=x3-0,2x2-1,5x+1. Gemäß der Klassifizierung von zuvor handelt es sich um eine ganzrationale Funktion 3. Grades.
Wir machen uns wieder anhand des Funktionsterms ein ungefähres Bild vom Verlauf des Graphen dieser ganzrationalen Funktion. |
| x |
-1000000 |
-100000 |
-1000 |
0 |
1000 |
100000 |
1000000 |
| f(x)=x3-0,2x2-1,5x+1 |
-1018 |
-1015 |
-109 |
1 |
109 |
1015 |
1018 |
| f(x)=x3 |
-1018 |
-1015 |
-109 |
1 |
109 |
1015 |
1018 |
Die zweite Tabellenzeile enthält die komplette Funktionsgleichung während in der dritten Tabellenzeile nur das erste Glied der Funktionsgleichung berücksichtigt ist. Die Berechnung der Funktionswerte zeigt sowohl für die komplette Funktions-gleichung als auch für die Rumpfgleichung dieselben Werte. Allerdings im Gegensatz zu geraden Werten von n stellen wir fest, dass, je kleiner der x-Wert wird, umso kleiner wird der f(x)-Wert. Und je größer x wird, umso größer wird der f(x)-Wert. Der Graph der Funktion verläuft von links unten nach rechts oben.
Betrachten wir jetzt das Verhalten von f nahe Null über die nachfolgend aufgeführte Tabelle: |
| x |
-0,1 |
-0,05 |
-0,01 |
0 |
0,01 |
0,05 |
0,1 |
| f(x)=x3-0,2x2-1,5x+1 |
1,147 |
1,074 |
1,015 |
1 |
0,985 |
0,925 |
0,849 |
| f(x)=-1,5x+1 |
1,15 |
1,075 |
1,015 |
1 |
0,985 |
0,925 |
0,85 |
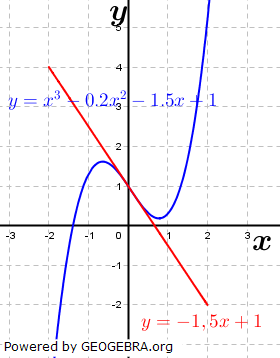 Die zweite Tabellenzeile enthält die komplette Funktionsgleichung während in der dritten Tabellenzeile nur die letzten beiden Glieder der Funktionsgleichung berücksichtigt sind. Die Berechnung der Funktionswerte zeigt sowohl für die komplette Funktionsgleichung als auch für die Rumpfgleichung ungefähr dieselben Werte. Das Verhalten nahe Null wird somit nur durch die letzten beiden Glieder beeinflusst, wie dies auch aus nebenstehender Grafik hervorgeht. Die zweite Tabellenzeile enthält die komplette Funktionsgleichung während in der dritten Tabellenzeile nur die letzten beiden Glieder der Funktionsgleichung berücksichtigt sind. Die Berechnung der Funktionswerte zeigt sowohl für die komplette Funktionsgleichung als auch für die Rumpfgleichung ungefähr dieselben Werte. Das Verhalten nahe Null wird somit nur durch die letzten beiden Glieder beeinflusst, wie dies auch aus nebenstehender Grafik hervorgeht. |




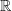 . Die Indices von an, an-1, an-2 usw. verweisen auf die Teilfunktion mit dem entsprechenden n als Exponent.
. Die Indices von an, an-1, an-2 usw. verweisen auf die Teilfunktion mit dem entsprechenden n als Exponent. .
.
 Wir betrachten zunächst eine Funktion mit n=4.
Wir betrachten zunächst eine Funktion mit n=4. . Gemäß der Klassifizierung von zuvor handelt es sich um eine ganzrationale Funktion
. Gemäß der Klassifizierung von zuvor handelt es sich um eine ganzrationale Funktion 


 Wir betrachten nun eine Funktion mit n=3.
Wir betrachten nun eine Funktion mit n=3. Die zweite Tabellenzeile enthält die komplette Funktionsgleichung während in der dritten Tabellenzeile nur die letzten beiden Glieder der Funktionsgleichung berücksichtigt sind. Die Berechnung der Funktionswerte zeigt sowohl für die komplette Funktionsgleichung als auch für die Rumpfgleichung ungefähr dieselben Werte. Das Verhalten nahe Null wird somit nur durch die letzten beiden Glieder beeinflusst, wie dies auch aus nebenstehender Grafik hervorgeht.
Die zweite Tabellenzeile enthält die komplette Funktionsgleichung während in der dritten Tabellenzeile nur die letzten beiden Glieder der Funktionsgleichung berücksichtigt sind. Die Berechnung der Funktionswerte zeigt sowohl für die komplette Funktionsgleichung als auch für die Rumpfgleichung ungefähr dieselben Werte. Das Verhalten nahe Null wird somit nur durch die letzten beiden Glieder beeinflusst, wie dies auch aus nebenstehender Grafik hervorgeht.

















