Quadratische Funktionen mit Parameter der Funktionsklassen - Aufgabenblätter/© by www.fit-in-mathe-online.de

Quadratische Funktionen mit Parameter Level 3 - Expert Aufgabenblatt 5

Dokument mit 22 Aufgaben

Hinweis:
In diesem Aufgabenblatt befinden sich Aufgaben zu quadratischen Funktionen mit Parameter.

Aufgabe A1 (3 Teilaufgaben)
Lösung A1

Aufgabe A1 (3 Teilaufgaben)

Gegeben ist f_t mit $Fit in Mathe Latex: 7ff02ff6675cab39dc818c9490024b61.png$ .
Welche der nachfolgend abgebildeten Schaubilder gehören zu einer Funktion f_t, welche nicht?
Begründe deine Entscheidung und ermittle gegebenenfalls den zugehörigen Wert von t.

Gegeben ist ft mit ft(x)=x^2-0,5t^2x+t; x,t ∈ R. (Grafik A350101 im Aufgabensatz 01 Blatt 3/5 Expert zu quadratischen Funktionen mit Parameter in den Funktionsklassen) /© by www.fit-in-mathe-online.de)

Welche der nachfolgend abgebildeten Schaubilder gehören zu einer Funktion ft, welche nicht? (Grafik A350102 im Aufgabensatz 01 Blatt 3/5 Expert zu quadratischen Funktionen mit Parameter in den Funktionsklassen) /© by www.fit-in-mathe-online.de)

Begründe deine Entscheidung und ermittle gegebenenfalls den zugehörigen Wert von t. (Grafik A350103 im Aufgabensatz 01 Blatt 3/5 Expert zu quadratischen Funktionen mit Parameter in den Funktionsklassen) /© by www.fit-in-mathe-online.de)

Aufgabe A2 (3 Teilaufgaben)

Gegeben ist für jedes a≠0 die Funktions f_a mit $Fit in Mathe Latex: 2d385fa80f7e9b2d98461ceee8c3a9ec.png$ . K_a ist das Schaubild von f_a.
a)	Betrachten Sie K_a für verschiedene Werte von a und geben Sie drei gemeinsame Eigenschaften an.
b)	Für welchen Wert von a ist die 1. Winkelhalbierende Tangente an K_a?
c)	Für welchen Wert von a ist 3 der größte Funktionswert?

Aufgabe A3 (4 Teilaufgaben)

Gegeben ist für 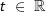$Fit in Mathe Latex: 0ad59570691ae273d8dc65c66863ac14.png$ die Funktion f_t mit $Fit in Mathe Latex: c8a42f5b2ee24be8a9d887ebe5661519.png$ . K_t ist das Schaubild von f_t.
a)	Zeichne K_t für drei verschiedene Werte von t.
b)	Wo schneidet K_t die Koordinatenachsen? Für welchen t–Wert hat f_t genau eine Nullstelle? Interpretiere.
c)	Der Schnittpunkt von K_t mit der x–Achse und der Punkt S(3\|-t) sind für 0<t<6 die Eckpunkte eines Dreiecks mit dem Inhalt A(t). Bestimme t so, dass A(t)=4 ist.
d)	Welche Ursprungsgerade ist Tangente an K₀?

Aufgabe A4 (2 Teilaufgaben)
Lösung A4

Aufgabe A4 (2 Teilaufgaben)

Bestimme die gemeinsamen Punkte der folgenden Funktionen in Abhängigkeit von t:
a)	$Fit in Mathe Latex: 69761cab2ae9a7b3764980f5a8028c7b.png$ und g(x)=1 mit $Fit in Mathe Latex: d181ea6d68fa7e2dcf215b165503e6bd.png$
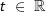b)	$Fit in Mathe Latex: a274c427b745c8da5fd5ee9f4cee3e57.png$ und g(x)=-x²+4x mit $Fit in Mathe Latex: 0ad59570691ae273d8dc65c66863ac14.png$

Aufgabe A5 (3 Teilaufgaben)

Gegeben seien die Funktionen $Fit in Mathe Latex: a143f75745068bfec904b80ca5f6325e.png$ und $Fit in Mathe Latex: f30fcf9fa5225d728d8a785bdfba5dfd.png$ .
a)	Berechne alle Achsenschnittpunkte von f.
b)	Berechne alle Achsenschnittpunkte von g_t in Abhängigkeit von t.
c)	Für welche t haben die Schaubilder von f und g_t
	-	zwei Schnittpunkte
	-	einen Berührpunkt
	-	keinen gemeinsamen Punkt?

Aufgabe A6
Lösung A6

Aufgabe A6

Welchen Wert muss t annehmen, damit das Schaubild der Funktion $Fit in Mathe Latex: bc0d263d18ff281c5b47b317d3769fd8.png$ die Gerade g(x)=-1 gerade berührt?
Bestimme die Koordinaten des Berührpunktes.

Aufgabe A7
Lösung A7

Aufgabe A7

Welchen Wert muss t annehmen, damit das Schaubild der Funktion f_t(x)=x²-tx+72 die nach unten geöffnete Normalparabel p(x)=-x² gerade berührt?
Bestimme die Koordinaten des Berührpunktes.

Aufgabe A8 (4 Teilaufgaben)

Bestimme die Gleichung der Ortskurve der Scheitelpunkte von f_t und zeichne die Ortskurve und die Schaubilder von f_t für t ∈ {-3;-2;-1;0;1;2;3} in ein gemeinsames Koordinatensystem.
a)	$Fit in Mathe Latex: 86aacd693f9df6fdb72b3141a1811597.png$ für -3 ≤ x ≤ 3 und -2 ≤ y ≤ 4.
b)	$Fit in Mathe Latex: 5de03551582af588852f707b1e6d6b80.png$ für -3 ≤ x ≤ 3 und -7 ≤ y ≤ -2.
c)	$Fit in Mathe Latex: 641eb3fabfa1cf6dcc12ccabd9f30c07.png$ für -3 ≤ x ≤ 3 und -2 ≤ y ≤ 7.
d)	$Fit in Mathe Latex: 06e6a9534189a230b8d6d84ef225d905.png$ für -2 ≤ x ≤ 6 und -2 ≤ y ≤ 6.

Aufgabe A9

Auf einer Cerealienpackung ist der Zugangscode für ein low-cost (d.h. von einem Informatikkurs programmierten) Computerspiel abgedruckt, dessen Hintergrundlandschaft durch die Parabeln $Fit in Mathe Latex: 4fd847355c0f411124ec25cf669ef3c4.png$ beschrieben wird.
Skizziere die Parabeln für t ∈ {±2; ±1;0} in ein gemeinsames Koordinatensystem und zeige rechnerisch, dass die Ortskurve der Scheitelpunkte sich durch die Gleichung $Fit in Mathe Latex: a69e4be300d19c729c4ce08b7471bad8.png$ beschreiben lässt.