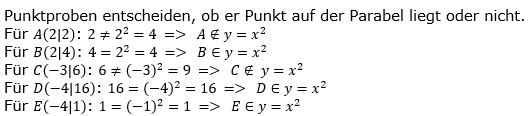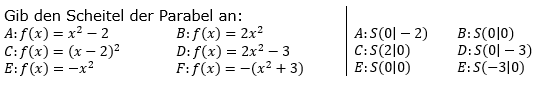 |
Quadratische Funktionen (Parabeln) Level 1 - Grundlagen - Aufgabenblatt 5 |
| Dokument mit 40 Aufgaben |
Aufgabe A1 (5 Teilaufgaben)
| Gib an, welche Punkte auf der Normalparabel y=x2 liegen: | ||||
| A(2|2) | B(2│4) | C(-3│6) | D(-4│16) | E(-1│-1) |
 Eine Frage stellen... |
Fehler melden...Aufgabe A2 (4 Teilaufgaben)
| Gegeben ist die Parabel mit der Gleichung y=5x2. Ergänze die Koordinaten so, dass die Punkte auf der Parabel liegen. Eventuell gibt es zwei Lösungen. |
A(1|…. ) | ........ |
 |
........ | |
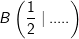| C(....|0 ) | ........ | |
| D(....|20 ) | ........ |
| Eine Frage stellen... |
Aufgabe A3 (6 Teilaufgaben)
| Gib den Scheitel der Parabel an: | |||
| A: f(x)=x2-2 | B: f(x)=2x2 | A: S(….|….) | B: S(….|….) |
| C: f(x)=(x-2)2 | D: f(x)=2x2-3 | C: S(….|….) | D: S(….|….) |
| E: f(x)=-x2 | F: f(x)=-(x2+3) | A: E(….|….) | B: F(….|….) |
| Eine Frage stellen... |
Aufgabe A4 (4 Teilaufgaben)
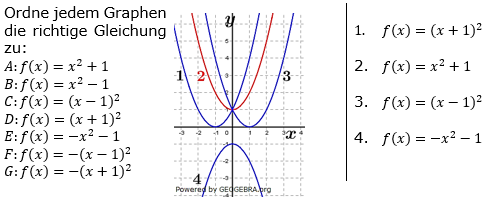
| Ordne jedem Graphen die richtige Gleichung zu: |  |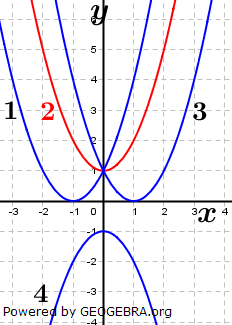
|
| 1. ________________________ | ||
| A: f(x)=x2+1 | 2. ________________________ | |
| B: f(x)=x2-1 | ||
| C: f(x)=(x-1)2 | 3. ________________________ | |
| D: f(x)=(x+1)2 | ||
| E: f(x)=-x2-1 | 4. ________________________ | |
| F: f(x)=-(x-1)2 | ||
| G: f(x)=-(x+1)2 |
| Eine Frage stellen... |
Aufgabe A5 (3 Teilaufgaben)
| Gib die Gleichung der verschobenen Normalparabel an : | |||
| a) | Die Parabel ist um 5 Einheiten auf der y-Achse nach unten verschoben. | a) | f(x)=_____________________ |
| b) | Die Parabel ist um 3,75 Einheiten in positive x-Richtung verschoben. | b) | f(x)=_____________________ |
| c) | Die Parabel ist an der x-Achse gespiegelt und anschießend um eine Einheit in positive y-Richtung verschoben worden. | c) | f(x)=_____________________ |
| Eine Frage stellen... |
Aufgabe A6 (3 Teilaufgaben)
| Gib den Scheitel der Parabel an : | ||
| A: | f(x)=(x-5)2+6 | A: S( | ) |
| B: |  |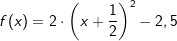
B: S( | ) |
| C: |  |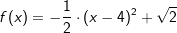
C: S( | ) |
| Eine Frage stellen... |
Aufgabe A7 (3 Teilaufgaben)
| S ist der Scheitel einer verschobenen Normalparabel. Gib die Gleichung des Graphen in Scheitelform an: | a) | f(x)=_____________________ | |||||
| b) | f(x)=_____________________ | ||||||
| a) | S(-2|3) | b) | S(5|12) | c) |  |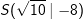
c) | f(x)=_____________________ |
| Eine Frage stellen... |
Aufgabe A8 (3 Teilaufgaben)
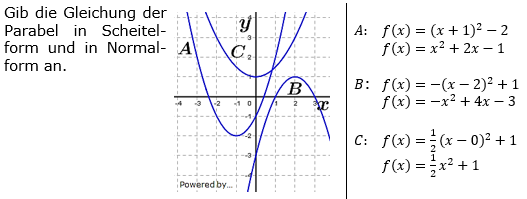
| Gib die Gleichung der Parabel in Scheitelform und in Normalform an. |  |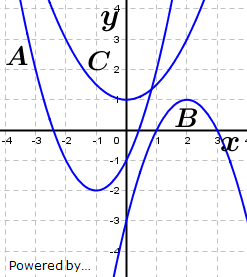
||
| A: | f(x)=________________ | ||
| f(x)=________________ | |||
| B: | f(x)=________________ | ||
| f(x)=________________ | |||
| C: | f(x)=________________ | ||
| f(x)=________________ |
| Eine Frage stellen... |
Aufgabe A9 (3 Teilaufgaben)
| Die Normalparabel mit f(x)=x2 wird so verschoben, dass ihr Scheitel in S(17|124) liegt. | A(19|….) | A(19|….) |
| B(16|….) | B(16|….) | |
| Ergänze die fehlenden Koordinaten so, dass die Punkte auf der verschobenen Parabel liegen. Prüfe jeweils, ob es zwei Lösungen gibt. | C(.....|133) | C(.....|133) |
| Eine Frage stellen... |
Aufgabe A10 (2 Teilaufgaben)
| a) | Berechne die Nullstellen der Funktion mit f(x)=x2-4x+3. | a) | x1= ______ | x2= ______ | |
| b) | Eine Parabel schneidet die x-Achse in P(-2|0) und Q(1|0). Welche x-Koordinate hat der Scheitel? |
b) | x= ______ |
| Eine Frage stellen... |
Aufgabe A11 (2 Teilaufgaben)
| Berechne die Scheitelkoordinaten der Parabel. Ist der Scheitel der höchste oder der tiefste Punkt der Parabel? | |||
| a) | S(…..|…..) | ||
| _______________________ | |||
| a) | f(x)=x2-2x-3 | b) | S(…..|…..) |
| b) | f(x)=-x2-x+6 | _______________________ | |
| Eine Frage stellen... |
Aufgabe A12 (2 Teilaufgaben)
| Bestimme den Scheitel S der Parabel mit der Gleichung f(x)=1,2x2-0,5x-0,125 und ihre Schnittpunkte P und Q mit der x-Achse. |
||
| S(…..|…..) | ||
| P(…..|…..) | Q(…..|…..) | |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Quadratische Funktionen (Parabeln) Level 1 - Grundlagen - Aufgabenblatt 5 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
