Gegeben sei die ganzrationale Funktion f mit 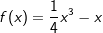 . .
Die Animation rechts zeigt den Graphen von f.
Betrachten wir den Punkt P sowie dessen „Spiegelpunkt“ P'.
Die Animation kann durch einen Klick auf "Start" gestartet werden, Klick auf "Pause" hält die Animation an, Klick auf "Weiter" setzt sie fort und ein Klick auf "Stop" zeigt wieder die Ausgangsstellung. |
|
Wir stellen fest, dass die y-Werte die jeweiligen Spiegel an der x-Achse, die x-Werte aber die jeweiligen Spiegel an der y-Achse.
Wir können hieraus den Merksatz für die Punktsymmetrie herleiten, nämlich
Merksatz Punktsymmetrie
|
Der Graph einer Funktion f mit der Definitionsmenge 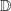 ist genau dann punktsymmetrisch zum Ursprung O(0|0), wenn für alle ist genau dann punktsymmetrisch zum Ursprung O(0|0), wenn für alle 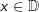 gilt: gilt: |
|
|
-f(-x)=f(x) |
|
|
|
Hinweis:
Im Schulbetrieb wird eigentlich gelehrt, dass f(-x)=-f(x) ist. Die hier aufgeführte Regel mit -f(-x)=f(x) ist identisch, denn die Multiplikation von f(-x)=-f(x) mit -1 führt ja zu -f(-x)=f(x). Letztere Formel führt jedoch zu einfacheren Berechnungen, wenn Symmetrie rechnerisch nachgewiesen werden soll. |





