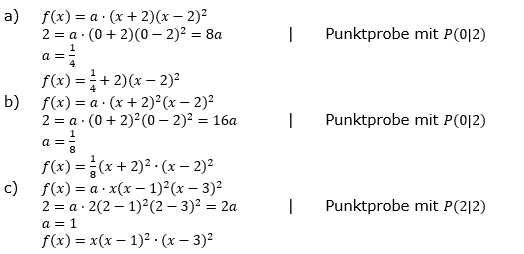 |
Nullstellen ganzrationaler Funktionen - Level 2 - Fortgeschritten - Blatt 2 |
| Dokument mit 33 Aufgaben |
Aufgabe A1 (3 Teilaufgaben)
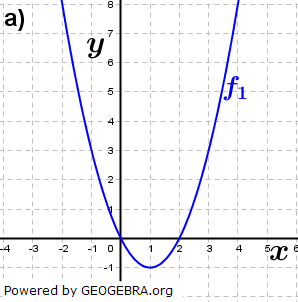
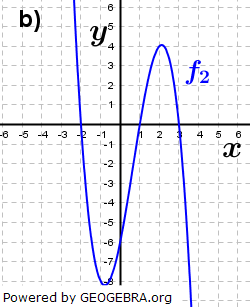
| Lies die Nullstellen an den Graphen ab und ermittle einen möglichen Funktionsterm. |
   |
 Eine Frage stellen... |
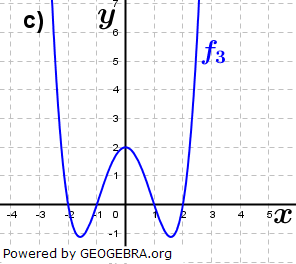Fehler melden...Aufgabe A2 (4 Teilaufgaben)
| Berechne die Nullstellen nachfolgender Funktionsgleichungen durch Faktorisieren und dem Satz vom Nullprodukt. In manchen Fällen musst du noch Substitution anwenden. |
 |
| Eine Frage stellen... |
Aufgabe A3 (4 Teilaufgaben)
| Bestimme die exakten Nullstellen durch Faktorisieren und dem Satz vom Nullprodukt. |
 |
| Eine Frage stellen... |
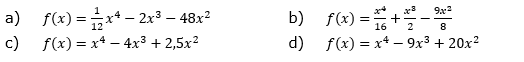Aufgabe A4 (4 Teilaufgaben)
| Bestimme die exakten Nullstellen durch Substitution und Resubstitution. |
 |
| Eine Frage stellen... |
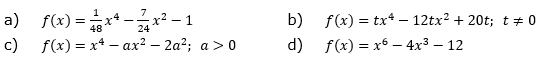Aufgabe A5 (6 Teilaufgaben)
| Löse die Gleichungen mithilfe einer Resubstitution. |
 |
| Eine Frage stellen... |
Lösungshilfe A6
| Haben wir es mit biquadratischen Gleichungen zu tun, so wird im allgemeinen die biquadratische Gleichung mit Substitution in eine rein quadratische Gleichung überführt, die dann mittels Mitternachtsformel gelöst wird. Ist diese Lösung bekannt, müssen dann die Lösungen der Gleichung mittels Resubstitution noch gefunden werden. Die Vorgehensweise Substitution / Resubstitution kann aber auf einfache Weise auch übergangen werden. Wer will uns denn verbieten, dass wir bei einer Gleichung von z. B. x4+bx2+c=0 die Mitternachtsformel direkt anwenden, wie im Folgenden gezeigt wird. |
||
| x4+bx2+c=0 | ||
 |
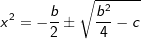p/q-Formel | |
| Somit haben wir die Substitutionsvariable lediglich durch x2 ersetzt. Und nach der Ausrechnung von x2 müssen wir dann nur noch die Wurzel des/der Ergebnisse(s) ziehen. Zum Studieren dieser Vorgehensweise siehe die nachfolgenden Lösungen. |
||
Aufgabe A7 (3 Teilaufgaben)
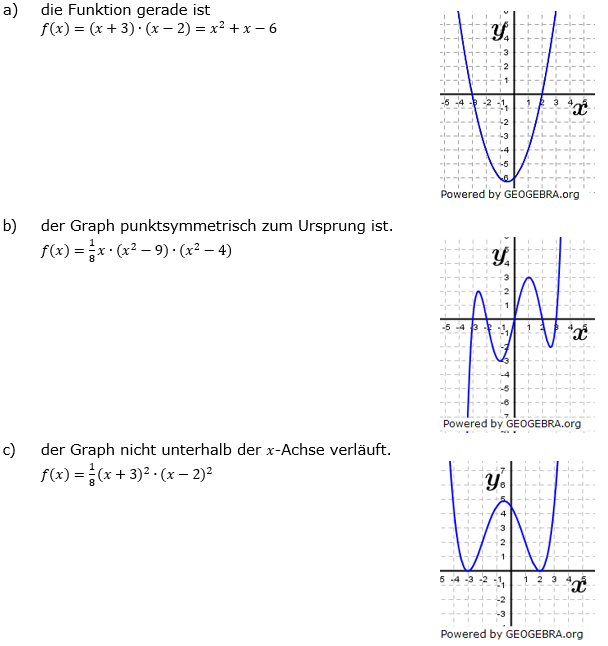
| Eine ganzrationale Funktion hat mindestens die Nullstellen x1=-3 und x2=2. Skizziere einen möglichen Graphen, wenn | |
| a) | die Funktion gerade ist. |
| b) | der Graph punktsymmetrisch zum Ursprung ist. |
| c) | der Graph nicht unterhalb der x-Achse verläuft. |
| Eine Frage stellen... |
Aufgabe A8 (4 Teilaufgaben)
| Für Aufgaben, bei denen die Nullstellen bzw. Linearfaktoren ganzrationaler Funktionen ermittelt werden sollen, werden aus den Linearfaktoren (x+2), (x-3) und (x-4) sowie dem Klammerausdruck (x2+1) Funktionsterme mit vorgegebenen Eigenschaften in ausmultiplizierter Form erzeugt. | |
| a) | Der Grad der Funktion soll 3 bzw. 5 sein. |
| b) | Die Funktion soll den Grad 4 bzw. 6 und genau zwei Nullstellen haben. |
| c) | Die Funktion soll keine Nullstellen und einen Grad größer als 3 haben. |
| d) | Die Funktion hat den Grad 4, das Absolutglied im Funktionsterm ist 12. |
| Eine Frage stellen... |
Aufgabe A9 (3 Teilaufgaben)
| Die Graphen gehören zu ganzrationalen Funktionen. Ermittle einen Funktionsterm. |
   |
| Eine Frage stellen... |
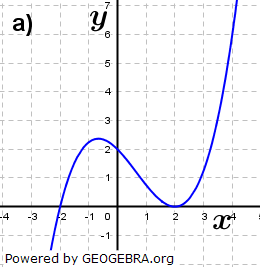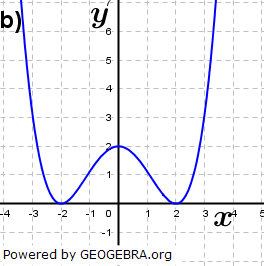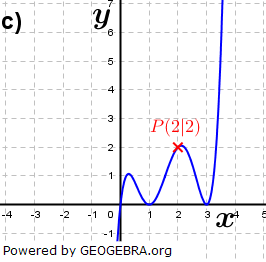Aufgabe 10 (3 Teilaufgaben)
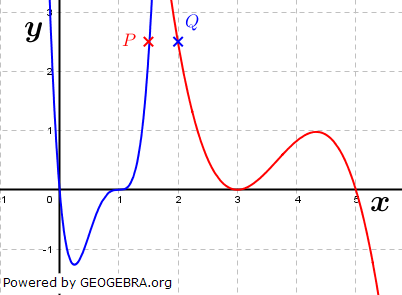 Die nebenstehende Graphik zeigt zwei ganzrationale Funktionen.Ermittle jeweils einen Funktionsterm. |
| Eine Frage stellen... |
| Du befindest dich hier: |
| Nullstellen ganzrationaler Funktionen - Level 2 - Fortgeschritten - Blatt 2 |
- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021
