|
Ganzrationale Funktionen mit Parameter - Level 3 - Expert - Blatt 2 |
| Dokument mit 24 Aufgaben |
Aufgabe A1 (3 Teilaufgaben)
| Bestimme diejenigen Werte von t, für die der Graph von f achsensymmetrisch zur y-Achse oder punktsymmetrisch zum Ursprung ist. |
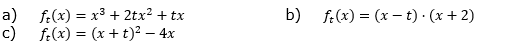 |
| |
Aufgabe A2 (3 Teilaufgaben)
| Bestimme alle Werte von t so, dass | |
| a) | die Funktion ft mit ft(x)=7(x-t)2⋅(x-2) eine dreifache Nullstelle hat. |
| b) | die Funktion ft mit ft(x)=(x+2)(x-t)(x-3)(x-4) eine doppelte Nullstelle hat. |
| c) | die Funktion ft mit ft(x)=5(x-2)(x-4)(x-t) die x-Achse berührt. |
| |
Aufgabe A3
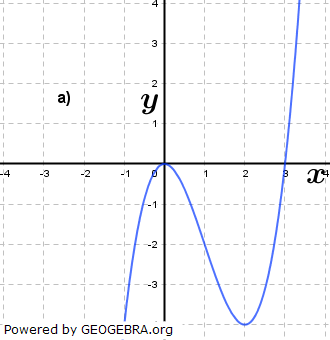
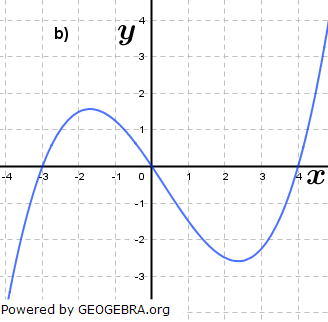
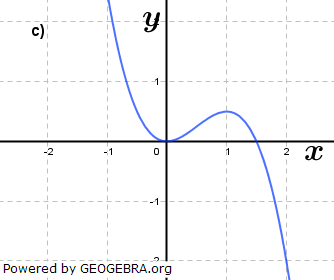
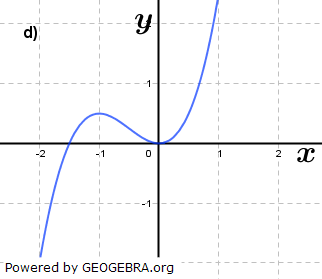
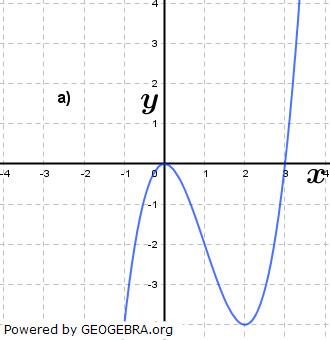
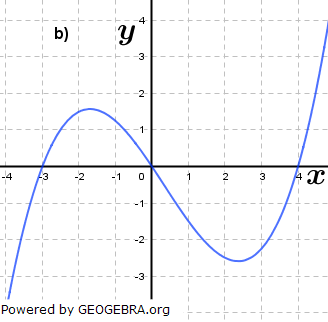
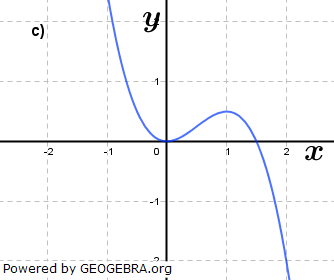
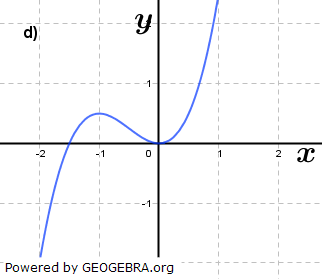
Gegeben ist für 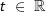 eine Funktion ft durch eine Funktion ft durch 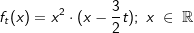 . Das Schaubild von ft ist Kt. Welche Schaubilder gehören zu einer Funktion ft, welche nicht? Begründe deine Entscheidung und ermittle gegebenenfalls den Wert von t. . Das Schaubild von ft ist Kt. Welche Schaubilder gehören zu einer Funktion ft, welche nicht? Begründe deine Entscheidung und ermittle gegebenenfalls den Wert von t.Fahre zum Vergrößern der Grafiken mit der Maustaste über die Grafiken. |
|||
 |
 |
 |
 |
| |
Aufgabe A4 (2 Teilaufgaben)
Zu jedem 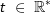 ist eine Funktion ft gegeben durch ist eine Funktion ft gegeben durch 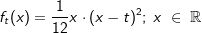 . Das Schaubild von ft ist Kt. . Das Schaubild von ft ist Kt. |
|
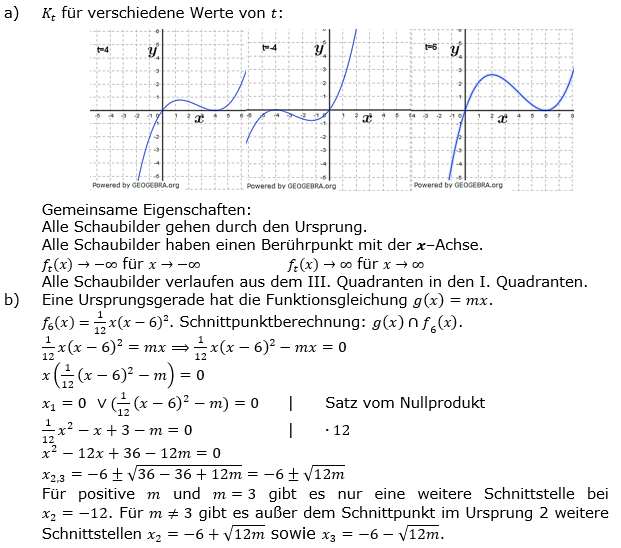
| a) | Betrachte Kt für drei verschiedene Werte von t. Gib gemeinsame Eigenschaften der Schaubilder an. Zeichne K6. |
| b) | Zeige, dass jede Ursprungsgerade mit positiver Steigung m und m≠3 K6 dreimal schneidet. |
| |
Aufgabe A5
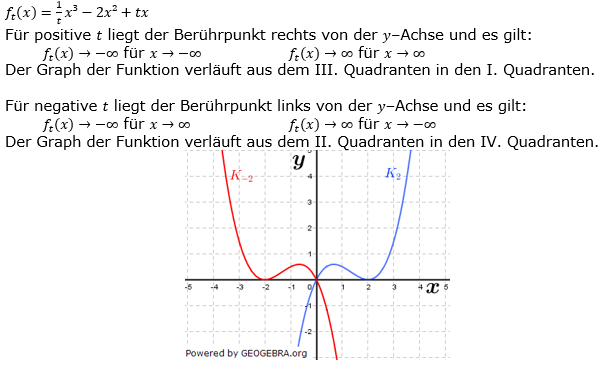
Für jedes 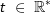 ist eine Funktion ft geben durch ist eine Funktion ft geben durch 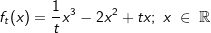 . Das Schaubild von ft ist Kt. . Das Schaubild von ft ist Kt.Betrachte Schaubilder für positive und negative Werte von t. Wie unterscheiden sich die Schaubilder für negative Werte von t von denen für positive Werte von t? Gib gemeinsame Eigenschaften der Schaubilder an. Skizziere zwei Schaubilder. |
| |
Aufgabe A6 (5 Teilaufgaben)
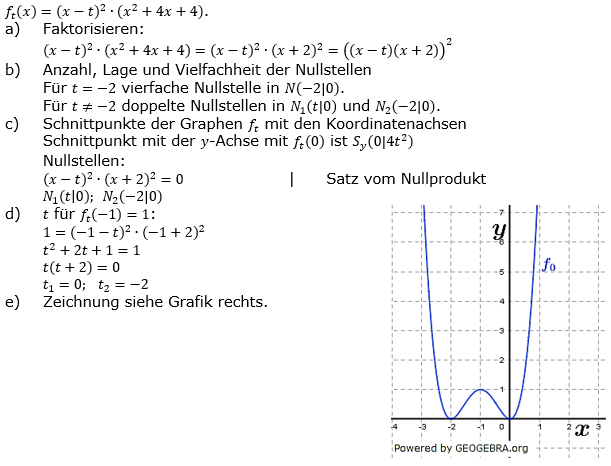
| Gegeben ist die Funktion ft mit ft(x)=(x-t)2∙(x2+4x+4). | |
| a) | Faktorisiere den Term so weit wie möglich. |
| b) | Gib mit Fallunterscheidung Anzahl, Lage und Vielfachheit der Nullstellen in Abhängigkeit von t an. |
| c) | Bestimme sämtliche Schnittpunkte der Graphen ft mit den Koordinatenachsen. |
| d) | Bestimme t so, dass der zugehörige Graph durch den Punkt P(-1|1) verläuft. |
| e) | Zeichne den Graphen f0 im Intervall [-3;1]. |
| |
Aufgabe A7 (4 Teilaufgaben)
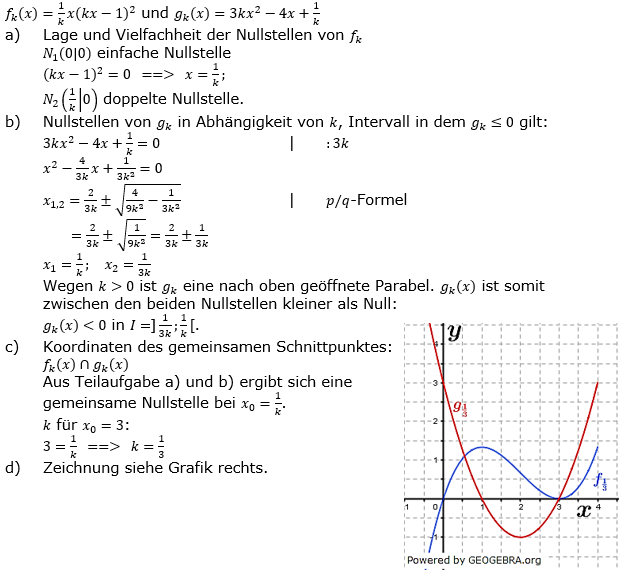
Die Funktion fk und gk mit k>0 sind gegeben durch 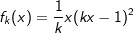 und und 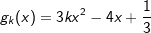 . . |
|
| a) | Gib die Lage und Vielfachheit der Nullstellen von fk an. |
| b) | Bestimme die Nullstellen von gk in Abhängigkeit von k und gib das Intervall an, in dem gilt gk≤0. |
| c) | Die beiden Funktionen haben eine gemeinsame Nullstelle. Gib die Koordinaten des gemeinsamen Schnittpunktes an und bestimme k so, dass die Abszisse des Schnittpunktes bei 3 liegt. |
| d) | Zeichne den Graphen von fk und gk für 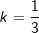 im Intervall [-1;4]. Für beide Koordinatenachsen gilt: 1 LE=2 cm im Intervall [-1;4]. Für beide Koordinatenachsen gilt: 1 LE=2 cm |
| |
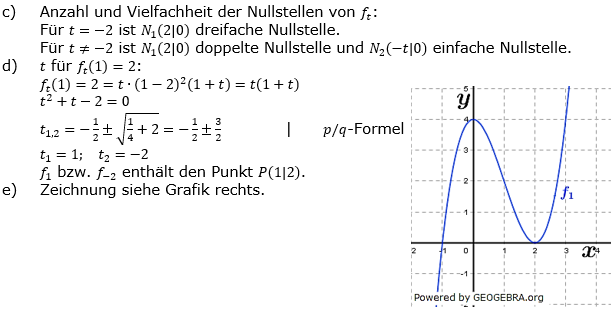
Aufgabe A8 (5 Teilaufgaben)
| Gegeben ist die Funktion ft durch ft(x)=t(x3+(t-4) x2+4(1-t)x+4t). | |
| a) | Zeige, dass ft eine Nullstelle bei 2 hat. |
| b) | Stelle ft in faktorisierter Form dar. |
| c) | Bestimme die Anzahl und Vielfachheit der Nullstellen von ft in Abhängigkeit von t. |
| d) | Berechne t so, dass P(1|2) auf ft liegt. |
| e) | Zeichne für t=1 den zugehörigen Graphen. |
| |
| Du befindest dich hier: |
| Ganzrationale Funktionen mit Parameter - Level 3 - Expert - Blatt 2 |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021