|
Potenzfunktionen - Level 2 - Fortgeschritten - Blatt 2 |
| Dokument mit 23 Aufgaben |
Aufgabe A1 (3 Teilaufgaben)
Gegeben sind die Funktionen f und g mit 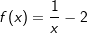 und und 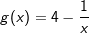 . . |
|
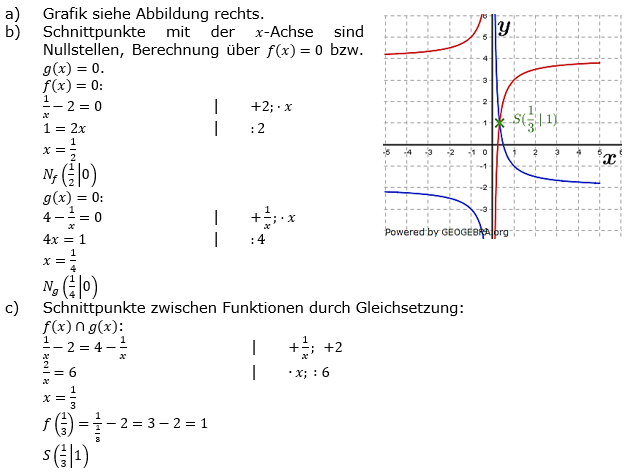
| a) | Zeichne die Graphen von f und g in ein geeignetes, gemeinsames Koordinatensystem. |
| b) | Berechne die Schnittpunkte von f und g mit der x-Achse. |
| c) | Wo schneiden sich f und g? Berechne den Schnittpunkt S. |
| |
Aufgabe A3
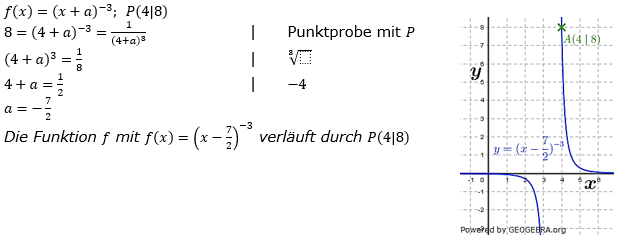
| Die Punkte A(7|1) und B(1|-1) liegen auf f mit f(x)=a∙(x+b)-1. Berechne a und b. |
| |
Aufgabe A4
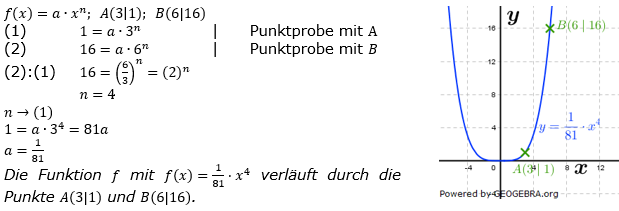
| Die Punkte A(3|1) und B(6|16) liegen auf f mit f(x)=a∙xn. Berechne a und n. |
| |
Aufgabe A5
| Gegeben sind die Funktionen f und g mit f(x)=xn+2,5 und g(x)=xm-5. f und g schneiden sich in S(2|3). Berechne n und m. |
| |
Aufgabe A6 (3 Teilaufgaben)
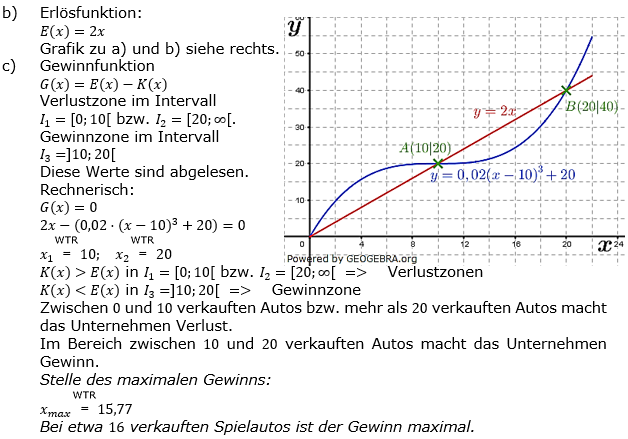
| Bei der Herstellung von Spielautos ergeben sich Kosten in Euro. Dabei sei K die Kostenfunktion mit K(x)=0,02⋅(x-10)3+20, K in Euro, x in Stück Spielauto. | |
| a) | Erstelle eine Wertetabelle mit x-Werten zwischen 0 und 22 und skizziere den Graphen für die Gesamtkosten K in Abhängigkeit der Stückzahl x. |
| b) | Der Artikel wird für € 2,00 / Spielauto verkauft. Wie groß sind die Einnahmen, wenn x Stück verkauft werden? Zeichne den Graphe für die Gesamteinnahmen in das vorhandene Koordinatensystem ein. |
| c) | Lies aus dem Graphen ab und berechne (falls möglich): • Bei welchen Stückzahlen wird Gewinn erzielt? • Bei welcher Stückzahl ist der Gewinn am größten? • Bei welchen Stückzahlen wird Verlust gemacht? |
| |
Aufgabe A7 (6 Teilaufgaben)
| Bestimme die Funktionsgleichung einer Potenzfunktion in der Form f(x)=a∙xq, deren Graph durch die genannten Punkte verläuft: | |||
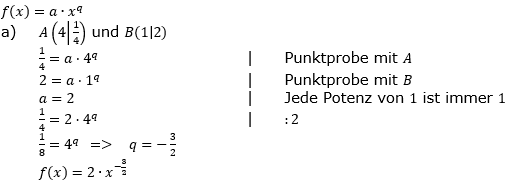
| a) | 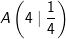 und B(1│2) und B(1│2) |
b) | A(2│8) und 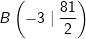 |
| c) | A(2│1) und 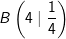 |
d) | A(4│4) und B(9│6) |
| e) | 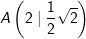 und B(2|4) und B(2|4) |
f) | A(4│1) und B(1│2) |
| |
Aufgabe A8 (4 Teilaufgaben)
| Gegeben sind die Funktionen f1, f2 und f3 mit f1(x)=(x+2)-2-3, f2 (x)=-(x-1)3+1,5 sowie f3(x)=-x4+1,5. Ihre Schaubilder sind K1, K2 und K3. | |
| a) | Ordne den abgebildeten Graphen den Funktionen zu und begründe deine Entscheidung. |
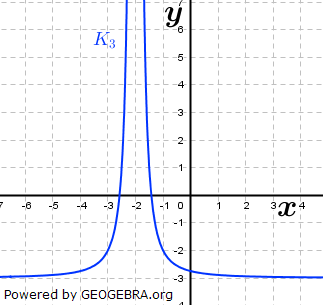 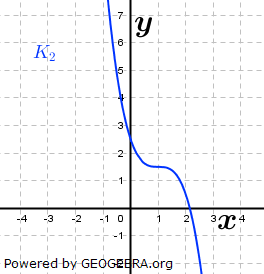 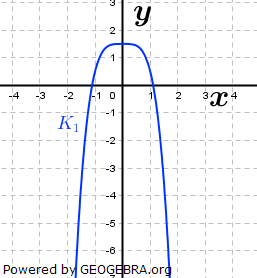 |
|
| b) | Berechne die Nullstellen von f1. |
| c) | Mache eine begründete Aussage zur Anzahl der Lösungen der Gleichung f3(x)=a, wobei a eine beliebige reelle Zahl sein kann. Die Begründung kann grafisch oder rechnerisch erfolgen. |
| d) | Für die Funktion, die zum Grafen K3 gehört, hat Emilie die Nullstellen x1=-5 und x2=4 berechnet. Was sagst du dazu? |
| |
Aufgabe A9
| In einer Publikation stand zu lesen: Der Durchmesser d eines Atomkerns hängt im Wesentlichen von der Anzahl A der Nukleonen (Protonen und Neutronen) ab. Wenn man sich den Atomkern als mehr oder weniger kugelförmigen Haufen aus Protonen und Neutronen vorstellt, kann man die folgende Näherungsformel für d (in m) verwenden: 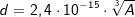 . .Ein Aluminiumkern hat 13 Protonen und 14 Neutronen. Wie groß ist sein Durchmesser in Millimeter? |
| |
Aufgabe A10 (2 Teilaufgaben)
| Aus einem Draht der Länge L soll das Gittermodell eines Würfels geformt werden. | |
| a) | Gib das Volumen eines Würfels in Abhängigkeit von L an. Stelle den funktionalen Zusammenhang grafisch dar. |
| b) | Welche Beziehung besteht zwischen L und der Oberfläche des Würfels? |
| |
| Du befindest dich hier: |
| Potenzfunktionen - Level 2 - Fortgeschritten - Blatt 2 |



- Geschrieben von Meinolf Müller Meinolf Müller
- Zuletzt aktualisiert: 16. Juli 2021 16. Juli 2021