Insgesamt gibt es (mit Stand Oktober 2010) in Deutschland rund 1,5 Millionen Kilometer Stromleitungen. Davon sind etwas weniger als 30 % sogenannte ‚Hochspannungs-‚ oder ‚Höchstspannungsleitungen’, das sind Leitungen mit Spannungen von 380000, 220000 und 110000 Volt. Ihre Gesamtlänge beträgt rund 116000 km. Wegen der sehr hohen Kosten und der schwierigen Wartung bei der unterirdischen Verlegung lassen sich diese praktisch nur oberirdisch verlegen. Im Mittel stehen dazu im Abstand von 300 bis 400 Metern die Masten, zwischen denen die einzelnen Kabel frei hängen. Insgesamt gibt es (mit Stand Oktober 2010) in Deutschland rund 1,5 Millionen Kilometer Stromleitungen. Davon sind etwas weniger als 30 % sogenannte ‚Hochspannungs-‚ oder ‚Höchstspannungsleitungen’, das sind Leitungen mit Spannungen von 380000, 220000 und 110000 Volt. Ihre Gesamtlänge beträgt rund 116000 km. Wegen der sehr hohen Kosten und der schwierigen Wartung bei der unterirdischen Verlegung lassen sich diese praktisch nur oberirdisch verlegen. Im Mittel stehen dazu im Abstand von 300 bis 400 Metern die Masten, zwischen denen die einzelnen Kabel frei hängen.
Die Messung der Höhe des Kabels über dem Boden in verschiedenen Abständen zum Strommast ergab bei einem Hochspannungskabel die folgende Wertetabelle:
| Abstand a in Metern |
20 |
40 |
60 |
80 |
100 |
120 |
| Höhe h in Metern |
42,8 |
39,8 |
37,2 |
35 |
33,2 |
31,8 |
|
| Eine quadratische Regression führte zur Funktionsgleichung |
| h(a)=0,0005a2-0,18a+46,2 |
| wobei a der Abstand in Metern von einem Hochspannungsmast aus gemessen, sowie h(x) die Höhe der Stromleitung über dem Boden in Metern ist. |
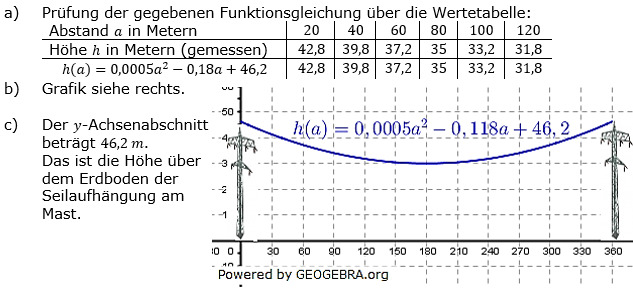
| a) |
Überprüfe, ob die gemessenen Wertepaare die Funktionsgleichung dieser quadratischen Funktion erfüllen. |
| b) |
Zeichne den Graphen dieser Quadratischen Funktion in ein geeignetes Koordinatensystem. |
| c) |
Gib den y-Achsenabschnitt dieser Quadratischen Funktion mit Maßeinheit an und erläutere die Bedeutung dieses Wertes für den Zusammenhang zwischen dem Abstand und der Höhe. |
| d) |
Berechne die Höhe des Kabels über dem Boden im Abstand von 200 m zum Strommast. |
| e) |
Berechne, in welchem Abstand zum ersten Strommast der zweite Strommast mit einer Höhe von 46,2 m steht. |
| f) |
Berechne, in welchem Abstand zum ersten Strommast das Kabel am tiefsten hängt und wie groß dort die Höhe über dem Boden ist. |
| g) |
Bekanntlich dehnen sich Hochspannungsleitung im Sommer aufgrund der Hitze aus und ziehen sich im Winter aufgrund der Kälte wieder zusammen. Gib an, welche Parameter des Funktionsterms sich beim Ausdehnen bzw. Zusammenziehen der Hochspannungsleitung ändern und begründe Deine Entscheidung. |

 Insgesamt gibt es (mit Stand Oktober 2010) in Deutschland rund 1,5 Millionen Kilometer Stromleitungen. Davon sind etwas weniger als 30 % sogenannte ‚Hochspannungs-‚ oder ‚Höchstspannungsleitungen’, das sind Leitungen mit Spannungen von 380000, 220000 und 110000 Volt. Ihre Gesamtlänge beträgt rund 116000 km. Wegen der sehr hohen Kosten und der schwierigen Wartung bei der unterirdischen Verlegung lassen sich diese praktisch nur oberirdisch verlegen. Im Mittel stehen dazu im Abstand von 300 bis 400 Metern die Masten, zwischen denen die einzelnen Kabel frei hängen.
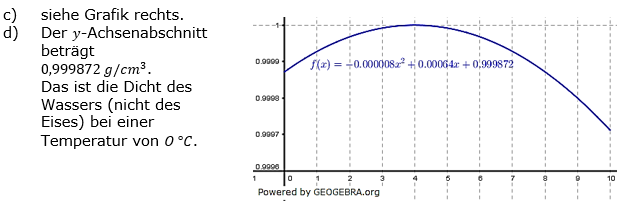
Insgesamt gibt es (mit Stand Oktober 2010) in Deutschland rund 1,5 Millionen Kilometer Stromleitungen. Davon sind etwas weniger als 30 % sogenannte ‚Hochspannungs-‚ oder ‚Höchstspannungsleitungen’, das sind Leitungen mit Spannungen von 380000, 220000 und 110000 Volt. Ihre Gesamtlänge beträgt rund 116000 km. Wegen der sehr hohen Kosten und der schwierigen Wartung bei der unterirdischen Verlegung lassen sich diese praktisch nur oberirdisch verlegen. Im Mittel stehen dazu im Abstand von 300 bis 400 Metern die Masten, zwischen denen die einzelnen Kabel frei hängen.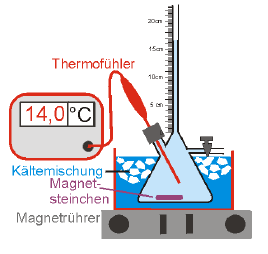 Wasser verhält sich bei kleinen Temperaturen über einem bestimmten Wert noch genau wie andere Flüssigkeiten: Bei Erhöhung der Temperatur wird die Dichte immer kleiner, bei Verringerung der Temperatur wird die Dichte immer größer. Unterhalb dieses Wertes jedoch hat Wasser eine besondere Eigenschaft, die es von fast allen anderen Flüssigkeiten unterscheidet und die für die Natur eine große Bedeutung hat. Diese spezielle Eigenschaft, die man die Anomalie des Wassers nennt, wird untersucht, indem man entsprechend dem rechts abgebildeten Versuchsaufbau eine bestimmte Menge Wasser langsam abkühlt und dabei ständig mit einem Thermofühler die Temperatur und anhand der Messung des Volumens und der Masse des Wassers dessen Dichte bestimmt.
Wasser verhält sich bei kleinen Temperaturen über einem bestimmten Wert noch genau wie andere Flüssigkeiten: Bei Erhöhung der Temperatur wird die Dichte immer kleiner, bei Verringerung der Temperatur wird die Dichte immer größer. Unterhalb dieses Wertes jedoch hat Wasser eine besondere Eigenschaft, die es von fast allen anderen Flüssigkeiten unterscheidet und die für die Natur eine große Bedeutung hat. Diese spezielle Eigenschaft, die man die Anomalie des Wassers nennt, wird untersucht, indem man entsprechend dem rechts abgebildeten Versuchsaufbau eine bestimmte Menge Wasser langsam abkühlt und dabei ständig mit einem Thermofühler die Temperatur und anhand der Messung des Volumens und der Masse des Wassers dessen Dichte bestimmt.